Triple Threat: Signal's Ratchet Goes Post-Quantum

---

---

tl;dr

Signal has introduced a new post-quantum ratchet in parallel to their existing double ratchet (one-way key evolution). It makes use of how ML-KEM works to optimize the process, with one party sending chunks of their public key in messages' headers while the other sends chunks of an encapsulated secret, then start over.

The shared secrets are input together with the outputs of the regular double ratchet into a key derivation function to derive the message keys.

Introduction

In the spring of 2022, we published two blog posts on secure messaging apps:

1. the first one covers, step by step, the basics of secure messaging, and
2. the second one focuses on group protocols.

We recommend having a look at these two posts if you would like to dive deeper on the subject, though a quick refresher will be provided here.

Several things have changed since then, of course, such as the Messaging Layer Security (MLS) mentioned in part 2 being standardized in 2023, as well as the NIST, after announcing the first four winners of its Post-Quantum Competition in the summer of 2022, publishing the first batch of standards in 2024.

Focusing solely on Signal, the changes that we are interested in are the additions of post-quantum cryptography (PQC) to its protocol. In 2023, Signal announced that their key agreement protocol, Extended Triple Diffie-Hellman (X3DH), was going to have a little brother, Post-Quantum Extended Diffie-Hellman (PQXDH), which we will talk about below. At that point, only the initial key agreement used quantum-resistant cryptography.

In early 2024, Apple announced that iMessage was also making the move to PQC and introduced PQ3, which secures both the initial key agreement and the following conversation with so-called ongoing PQC rekeying.

Other secure messaging apps were yet to follow.

Now, in early October 2025, Signal has announced that their ratcheting mechanism was also being upgraded with PQC in the beautifully acronymed Sparse Post Quantum Ratchet (SPQR).

We will first quickly recap the current situation with regard to the quantum threat, then recall the inner workings of Signal, and finally take a look at how SPQR works.

Quantum

Long story short: once quantum computers reach a certain size and level of stability, they will be able to break most of the public-key cryptography that we use today. More specifically, they could break the cryptography commonly used for key establishment.

Simply, Basic Crypto

Public key cryptography is also called asymmetric cryptography: for encryption, the sender uses the recipient's public key; and the recipient will use the corresponding private key to decrypt the message. This is useful when two parties have no prior relation but it is quite costly in performance and has a limited message size, so asymmetric crypto is generally used to establish a shared secret that will then be used for symmetric cryptography where the same key is used to encrypt and decrypt messages.

Most public-key algorithms rely on hard mathematical problems that modern computers cannot solve within a reasonable time frame — but as regular computers and algorithms do improve, we still increase key sizes regularly for RSA, for example — and that quantum computers could break efficiently some day. Symmetric cryptography is less affected by that problem, and is generally left aside when discussing the quantum threat.

PQC relies on different hard mathematical problems which are believed to be resistant to quantum attacks. Academics and researchers have worked on the subject for a long time now, and the NIST competition, which started in 2016, had the goal of standardizing some of these new algorithms in order to facilitate the adoption.

The migration towards PQC, like all transitions, takes time, hence the need to start early. The solution to ease the process is to use hybrid mode, a mix of classical and post-quantum cryptography, ensuring that the security of the protocol is not weakened against current threats while preparing for quantum ones.

For example, the ANSSI, the French national cybersecurity agency, has a 3-phase plan : in the first phase, which is now ending, PQC was only recommended for data that must remain confidential after 2030; the second phase, which has already started, makes hybrid schemes mandatory for security products, with security visas such as CSPNs being possibly granted for hybrid solutions; and finally, the third phase, which should start in 2030, will see the deprecation of non-PQC solutions.

The main concern here, and the reason quoted by Signal for the change, is the so-called "harvest now, decrypt later" attack where an adversary records some encrypted data in order to access its content later on, when advances in quantum computing may break the cryptography protecting said data. With long-lived conversations containing a lot of confidential information, which is often the case with secure messaging, the threat is very real.

Signal 101

As mentioned above, Signal has two main components: the initial key exchange, and then the ongoing key derivation for message encryption, called ratcheting. The name "ratchet" comes from the fact that the key can only evolve forward, i.e., knowing the key at a time $t$ does not allow you to compute the key at time $t-1$.

Forward, Backward

Two very important notions in secure messaging are forward secrecy and post-compromise security (or backward secrecy).

• Forward secrecy (FS): messages sent now remain secure if the session is compromised in the future. \
• Post-compromise security (PCS): messages sent after a compromise are secure (usually after a given delay).

Initial Key Exchange

Signal is fully asynchronous, meaning users do not, at any point, need to be online at the same time. For this reason, users need to store on a server (authenticated) public keys that can be fetched by someone wanting to start a conversation with them. In order to remain cryptographic, we will use the classical Alice and Bob example, where Alice wants to start a conversation with Bob.

When registering to Signal, Bob sent several public keys to the server (keeping the private keys on his device):

• a long term identity key $IK_B$, using classical cryptography (elliptic curves),
• a medium term signed prekey $SPK_B$, still using classical cryptography,
• a medium term signed "last resort" prekey $PQSPK_B$, using post-quantum cryptography,
• several one-time prekeys $OPK_{B,i}$, using classical cryptography,
• several signed one-time prekeys $PQOPK_{B,j}$, using post-quantum cryptography.

In the classical X3DH, only the keys using classical cryptography (currently curve25519 or curve448) are there. The PQC prekeys are meant to be used in a Key-Encapsulation Mechanism (KEM), currently ML-KEM (standard, based on NIST competition winner CRYSTALS-Kyber).

I'm Just KEM

A KEM uses asymmetric cryptography to establish a shared secret between two parties. Let $(pk,sk)$ be a public/private key pair, then when given $pk$ as input, the KEM encapsulation will output a random secret $k$ and a ciphertext $c$, such that the KEM decapsulation, when given $sk$ and $c$, will output $k$.

That way, the sender can use the recipient's public key to generate a shared secret, and send the ciphertext to the recipient, who will recover the secret via their private key.

When Alice wants to start a conversation with Bob, the server will send her some of Bob's public keys in a bundle:

$$\{IK_B, SPK_B, PQOPK_{B,j}\ or\ PQSPK_B, OPK_{B,i}\}$$

The one-time prekeys (one classical, one post-quantum) are used if available then deleted from the server; if there are no post-quantum ones left, the last-resort post-quantum prekey is sent (and not deleted).

Alice generates an ephemeral key pair of her own $(EPK_A,EK_A)$ and a shared secret $K$ using Bob's post-quantum prekey $PQPK_B$ (either the one-time prekey or the last-resort prekey) as input to the KEM. She then computes four Diffie-Hellman shared secrets using her private identity key $IK_A$, her ephemeral key $EK_A$, and Bob's public keys, and concatenates them with $K$ to derive the final shared secret $SK$ via a Key Derivation Function (KDF).

Diffie-Hellman

The most common way to obtain a shared secret based on two users' public/private key pairs is Diffie-Hellman (DH). Alice has her public/private key pair $(pk_A,sk_A)$ and receives Bob's public key $pk_B$, she computes the shared secret $k = \mathsf{DH}(sk_A,pk_B)$, and Bob obtains the same shared secret on his side by computing $k = \mathsf{DH}(sk_B,pk_A)$. If Alice's key pair is $(g^a,a)$ and Bob's key pair is $(g^b,b)$, then the shared secret is $k = g^{ab} = g^{ba}$.

Recall that obtaining $a$ from $g^a$ is the discrete logarithm problem, which is hard for classical computers, but can be solved efficiently by a quantum computer using Shor's algorithm.

$$SK = \mathsf{KDF}(\mathsf{DH}(IK_A, SPK_B) || \mathsf{DH}(EK_A, IK_B) || \mathsf{DH}(EK_A, SPK_B) || \mathsf{DH}(EK_A,OPK_B) || K)$$

The fourth DH is only computed if a one-time (classical) prekey was available. Alice sends Bob a message with her public identity key and public ephemeral key, as well as the ciphertext $CT$ from the KEM encapsulation so that Bob can recover $K$. Bob can then compute the same shared secret $SK$ using his private keys and Alice's public keys.

Detailed security considerations can be found in Signal's PQXDH specifications. We do recommend taking a look if you're interested in the subject, as well as the formal verification done by Cryspen.

Once the initial shared secret is established, Alice and Bob can exchange messages using Signal's ratcheting mechanism. Note that Alice can start sending messages right away, as she can compute the shared secret with just the bundle sent by the server.

Ratcheting Mechanism

Signal's protocol is based on the Double Ratchet algorithm, also used (directly or slightly modified) by many other secure messaging apps, such as WhatsApp or Matrix.

As mentioned above, a ratchet is a mechanism that only "goes forward", and Signal uses a chain of keys derived from each other — aptly called a "key chain" — via a one-way Key Derivation Function (KDF). In Signal, the two parties (Alice and Bob) each keep a receiving key chain and a sending key chain. Alice's sending chain is Bob's receiving chain, and vice-versa.

There are two types of ratchets (hence the name) :

• a symmetric one that is used for every new message; to advance the ratchet, only the current key is used as input, it brings forward secrecy;
• an asymmetric one, which is used regularly to restart the chains, taking as input one current key and a new random Diffie-Hellman key, bringing post-compromise security.

For the asymmetric ratchet, the users take turns in generating the new DH key pair, and sending the public key to the other party. This starts a new sending chain for the user who generated the new key pair, and thus a new receiving chain for the other user.

The chain of asymmetric ratchets is called the root chain, because it outputs the root keys of the sending/receiving chains.

Let us follow through a few messages in a simplified example, on Alice's side. We omit one key derivation: in reality the key in the sending/receiving chain is not used directly to encrypt/decrypt the messages.

Alice's storage contains:

• current public key from Bob $PK_{B,i}$,
• current private key $SK_{A,i}$,
• current receiving chain key $RK_{A,j}$,
• current sending chain key $NK_{A,k}$.

We now unroll a few steps.

1. Alice sends a new message to Bob, she derives $NK_{A,k}$ to get $NK_{A,k+1}$, and uses it to encrypt the message.
2. She sends a few more, each time deriving the sending chain key up to $NK_{A,k+n}$.
3. Bob replies, and sends his new public key $PK_{B,i+1}$.
4. Alice computes the new root key using her old private key $SK_{A,i}$ and Bob's new public key $PK_{B,i+1}$, and derives it to start a new receiving chain with key $RK_{A,j+1}$ which is not linked to $RK_{A,j}$.
5. She keeps advancing the receiving chain to decrypt Bob's new messages.
6. She generates a new key pair $(PK_{A,i+1}, SK_{A,i+1})$ and sends $PK_{A,i+1}$ to Bob.
7. She computes the new root key using her new private key $SK_{A,i+1}$ and Bob's current public key $PK_{B,i+1}$, and derives it to start her new sending chain.

An adversary that obtains the content of Alice's storage at a given time $t$ and then the encrypted messages cannot "go back in time" (FS), but they are able to advance the receiving and sending chains up until the moment Alice generates a new random DH key pair, which, by definition, cannot be computed ahead of time (PCS).

Now a quantum adversary could not break the symmetric ratchet, but it could break the asymmetric ratchet by obtaining the shared secret just from observing the exchanged messages' public keys. This can lead to the "harvest now, decrypt later" attack mentioned above.

SPQR

To prevent such an attack, Signal has introduced SPQR, which adds a third, post-quantum ratchet to the other two. As in PQXDH, the post-quantum ratchet uses a KEM (again, ML-KEM) to derive the shared secret.

The general principle is as follows. Alice, upon initiating the conversation with Bob, will generate a first post-quantum key pair with public key $EK$. She will send $EK$ to Bob along with her first message. Bob, when answering (and if his application/device supports SPQR), will use a KEM to compute $(CT,K) = \mathsf{KEM.Encaps}(EK)$, and send $CT$ to Alice, who can then recover $K = \mathsf{KEM.Decaps}(SK,CT)$. Alice will then generate a new post-quantum key pair, then Bob will encapsulate a new secret, and so on.

Practicalities

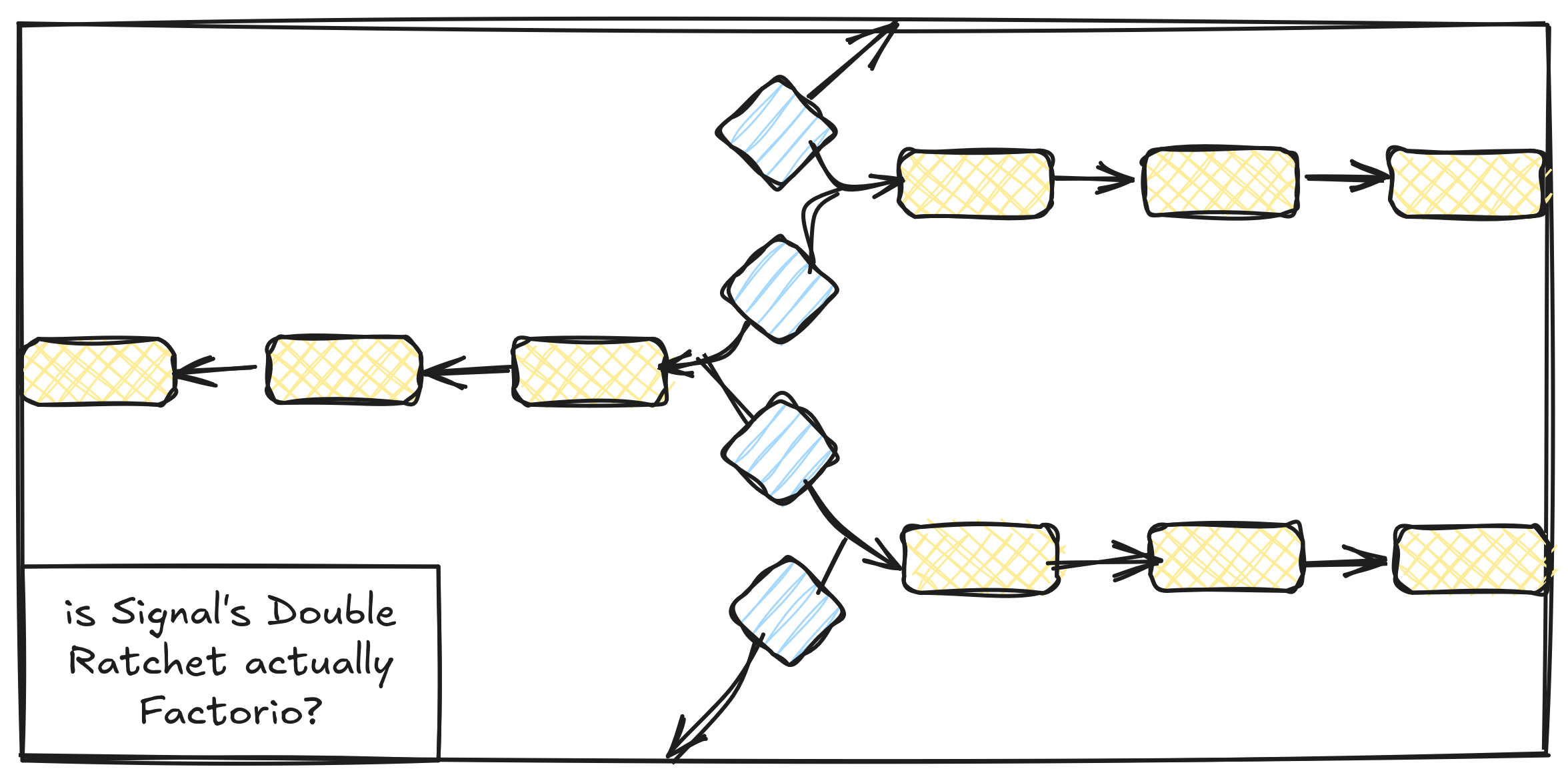
Now recall that post-quantum schemes are generally more costly than classical cryptography, and in order to save some resources, this post-quantum ratchet is not carried-out for every message, and even when renewed, Alice's $EK$ or Bob's $CT$ are not appended in full to a message.

Instead, they are cut up into chunks and sent over several messages, using eraser codes (a type of error correction that allows the recovery of the data as long as enough chunks are received, no matter which ones).

The initial idea is that Alice starts by adding a chunk of $EK$ with every message she sends until Bob has been able to reconstruct it, and generate a new $CT$, which he then chunks up and sends to Alice, until she can reconstruct it and send a new $EK$, and so on.

To optimize the process (without introducing new vulnerabilities, as nicely detailed step by step in Signal's SPQR blog post), the inner workings of ML-KEM are utilized: the encapsulation algorithm works in a way that Alice can send first a part of $EK$ (Seed) and a Hash, which Bob will use to generate the first part of $CT$, then Alice will send the rest of $EK$, used by Bob to generate the rest of $CT$.

That way, Bob is only "silent" in terms of Post-Quantum while Alice sends the first part and she is only "silent" while Bob finishes sending the rest of $CT$, instead of both being "silent" while waiting for the entire $EK$ or $CT$.

Tripling the Ratchet

Now that we have established a shared secret via the new post-quantum ratchet, it needs to be integrated into the existing Double Ratchet. Easily enough, the new shared post-quantum secret is simply input together with the output of the Double Ratchet into a KDF to derive the new message key.

In order to efficiently rollout this third ratchet, it is implemented in a way that allows immediate downgrade, i.e., if Alice sends an initial message that uses SPQR but Bob does not support it, he can still read the first messages without having to wait for Alice to downgrade and send them again.

And with that, Signal's underlying key establishments are fully post-quantum secure, from their wizard hat to their cowboy boots.

Sources

Signal documentation

• the blog post announcing PQXDH, the post announcing SPQR
• specifications for PQXDH, and SPQR

Cryspen

• formal verification of PQXDH
• formal verification of SPQR

Acknowledgments

I would like to thank my wonderful colleagues at Quarkslab for their reviews and suggestions, as well as Laurent Grémy for our past, current, and future discussions on the matter.