Authors Angèle Bossuat, Laurent Grémy
Category Cryptography
Tags secure messaging, privacy, cryptography, 2022
Today's communications are, as frequently requested by users, more and more secure. In this first part of the blogpost, we will detail some key features of instant messaging applications, in the setting where (only) two parties want to communicate.
Since time immemorial, (wo)men have wanted to communicate with each other, sometimes securely. At Quarkslab, we are extensively using emails and instant messaging systems, and we want (most of) our conversations to be confidential between all participants. In this blogpost, we will describe how to achieve end-to-end encryption, based on some realistic examples, in particular on our mattermost plugin.
Disclaimer: we will speak about cryptography, but we swear to not (extensively) use the cryptic language of Mordor!
Introduction
End-to-end encryption is one of the most common features instant messaging applications will now propose, even if people using them are not completely aware of the advantages or disadvantages that may come with this feature. It is the default mode of some of the most popular instant messaging applications: Signal, WhatsApp, Wire, Session (our audit), ...
A typical use case of these applications is textual conversation (1-on-1 or group) between the entities, and we will focus on that aspect in this blog post. This implies that people do not see each other, and thus cannot be sure that someone is not stalking their messages or impersonating one of the participants. In addition, communications are done through internet channels (mostly) on mobile devices, and the attack surface for these applications is huge! Cryptographic protocols are necessary pieces of this big puzzle, but they are not sufficient to communicate securely.
This blog post is not about the best or most secure instant messaging applications, but about the protocols they may use. We suggest referring to the Quarkslab comparison, Wikipedia or Secure Messaging Apps Comparison for help finding the most adequate application for your needs. Note also that the best application in your specific context is not necessarily the best for others', and this is why the correct answer to "what's the most secure messaging app out there?" is "well, it depends"...
In this blog post, we also use the Verifpal tool on a bunch of examples. Verifpal is a "starter pack" for symbolic verification: an easy-to-use, easy-to-understand verification software that can help us understand a protocol better, as well as provide some sanity checks on the security properties.
- Note:
Secure messaging applications have been analyzed formally mostly in the computational model (based on complexity theory, done by hand): we can for example cite the first analysis of Signal [CGCDGS16], more recently that of iMessage [BS20], and many others, often not focusing on one protocol in particular but on the theory behind it [BCSJNS17]. However, as discussed in [CGC17], messaging protocols, especially in the group setting (see our future blogpost on the subject, coming soon to a computer near you), are becoming too complicated to be done without the assistance of a tool, i.e. in the symbolic model: this has for example been done in [CFKN20] using Tamarin, or in [KBB17] using both ProVerif and CryptoVerif (the latter being an automated tool in the computational model).
Both models require some hands-on knowledge in order to prove anything, and both the modeling part and the result-interpretation part can be daunting: Verifpal is a good first step for newbies as it allows easy modeling and (partially) human-readable results, and though it is not as powerful or expressive as the other solutions, a sanity check is better than no check at all.
Once upon a time, A(lice) and B(ob)
Let us begin with the simplest (but not trivial) way to communicate: a conversation involving two entities, A and B.
If we imagine that A and B previously shared a secret s, then they can use an authenticated encryption algorithm, for example AES-GCM or Chacha20-Poly1305, to encrypt the messages. Let us see how we can proceed, with a first protocol P0:
A and B use a Key Derivation Function (KDF) on the secret s to derive a session key k;
A writes a message mA0, encrypts it with the key k and sends the encrypted message eA0 to B;
B decrypts eA0 with the key k and is now able to read the message;
B writes a message mB0, encrypts it with the key k and sends the encrypted message eB0 to A;
A decrypts eB0 with the key k and is now able to read the message;
...
We provide a Verifpal model of this protocol P0, along with the output. One of the abilities of the attacker is to duplicate some messages. In P0, there is no cryptographic way to detect the replacement of eB0 with eA0. In addition, if the secret s leaks, the attacker will be able to decrypt all of the messages, past and future. Let us first address the problem of decrypting past messages, which also solves the problem of "swapping" messages.
Server
In the following descriptions, we suppose that there exists a server that transmits the messages, which also allows to store the messages when the recipients are offline. As such, the server is a really good candidate to perform a man-in-the-middle attack. The attacker can then be "the system", and not only a router for the messages. Note that we do not address the metadata storage, which may reveal sufficiently many private information, even if the content of the messages remains unknown to the server. We do not address the network problems that may arise either (accidentally or maliciously).
Perfect forward secrecy
A system provides perfect forward secrecy (PFS) if compromising the current secrets of a user does not allow an attacker to decrypt the messages exchanged before the attack or the leak.
Ephemeral stories
In 1976, Diffie and Hellman published the well-known Diffie–Hellman–Merkle protocol [DH76] [Hel02]. It allows, in particular, to exchange a common secret key confidentially over a public channel. In the current state of our protocol, authenticity of the interlocutors and perfect forward secrecy are not yet achieved. One way to achieve that is to use the Station-to-Station protocol [DvOW92]; a simple, but close-to-reality, way to reach perfect forward secrecy is to:
use the permanent cryptographic material only to sign messages;
draw a new session key for each session.
Here is how to evolve P0 into a simplified ephemeral Diffie–Hellman–Merkle (DHE) protocol P1. We first consider that A owns the asymmetric key pair (skA, pkA) and B the pair (skB, pkB), where pkA and pkB are the public keys. We assume that A and B have previously authenticated each other's public key.
A draws a random ephemeral key pair (eskA, epkA), computes sA to be the signature of epkA by the private key skA and sends epkA and sA to B;
B verifies the signature sA with epkA and pkA;
B picks a random ephemeral key pair (eskB, epkB), computes sB to be the signature of epkB by the private key skB and sends epkB and sB to A;
A verifies the signature sB with epkB and pkB;
A computes the session key k using eskA and epkB, B computes the same session key using eskB and epkA.
Note that a Diffie–Hellman–Merkle key-exchange must be done for every message, as shown in this protocol model, and its output: indeed, at this stage, the only way to go from one session key to another is to perform a DHE for every message.
The protocol P1 is synchronous when building the encrypting key. Based on P1, an asynchronous protocol P2 can be proposed, which is close to the one we implemented in the e2ee Mattermost plugin. Let us consider now that A owns two asymmetric key pairs:
(skA, pkA) to sign;
(xskA, xpkA) to perform the key exchange.
B is in possession of two similar key pairs, respectively (skB, pkB) and (xskB, xpkB), and all of the public keys are authenticated by the two parties. The process for A to send an encrypted message to B is:
draw a random session key MK and an initial vector IV;
encrypt (not with an authenticated encryption algorithm) the message to be sent with MK and IV;
draw a random ephemeral key pair (keyECDHE, pubECDHE);
compute the shared secret DHSS using keyECDHE and xpkB and derive a key KWK from DHSS;
encrypt MK with KWK to get encryptedKey;
sign the concatenation of IV, pubECDHE, the public key identifier (basically the hash of pkB || xpkB) and the encrypted message.
With such a protocol P2, the communication may be done asynchronously, since the DHE used to derive the session key may be done by both parties at any time. However, the protocol P2 only achieves partial PFS: indeed, if the secret material of B leaks, it is impossible for an attacker to decrypt the message he sent in the past; but if it is the material of A that leaks, the attacker is able to decrypt all the messages she received.
One ratchet
To fully (i.e. on both sides) obtain PFS asynchronously, it is possible to use the Signal protocol [DR]. Let us consider that A and B already agreed on a shared secret s – how s is obtained is described in the next section.
The idea here is to let the session keys evolve from a common root, without reseeding them every time. To evolve from one session key to the next, a KDF is used: applying the KDF on the current key yields the key used to encrypt the next message. The KDF used in Signal is described as a ratchet (or a one-way function): indeed, one of the properties of that KDF is that, given the current session key, it is impossible to compute the previous session key (i.e. the one used to compute the current key). This gives the following chain:
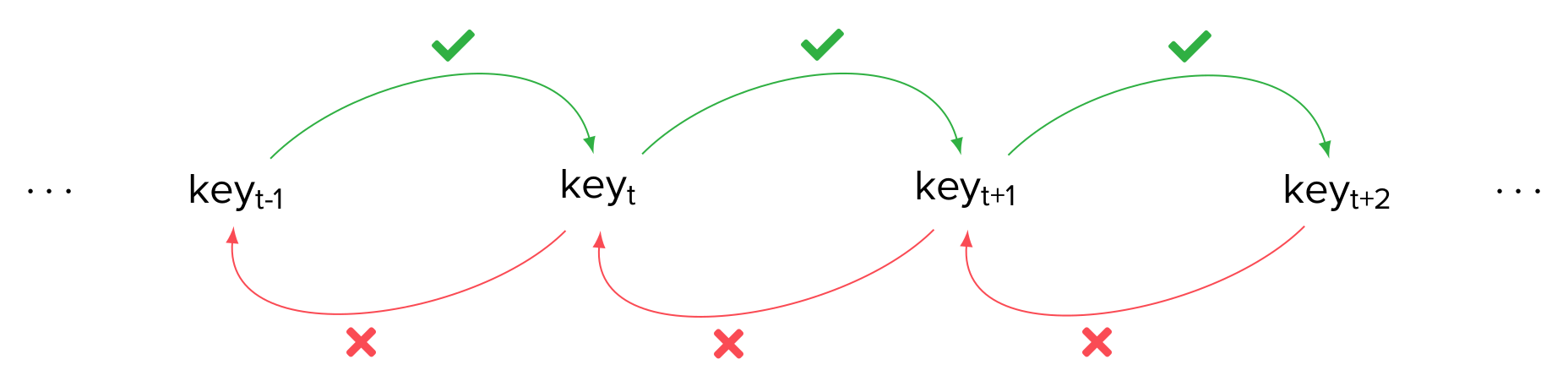
The new protocol P3 is the following:
A and B both compute the secret key k0 using a KDF on s;
A encrypts the message m0 with the key k0 and sends the encrypted message to B;
B decrypts the message using k0;
A and B compute the next secret key k1 using a KDF on k0;
B encrypts the message m1 with the key k1 and sends the encrypted message to A;
...
Note that in this situation, we have a walkie-talkie like conversation (push-to-talk or press-to-transmit). Since it is not convenient for most use cases, A and B must maintain two (symmetric) ratchet chains, one for each direction of the messages:
the emission chain of A is synchronized with the reception chain of B;
the emission chain of B is synchronized with the reception chain of A.
Beware: the name "double ratchet" of the Signal protocol does not refer to these two chains, but to yet another one, which is described below in Post compromise security.
Compared to the previous solution P2, the Signal protocol also needs less bandwidth, but the emission and reception chains need to evolve synchronously, which is another type of problem that we do not discuss here. Except for the agreement on the shared secret s, the protocol P3 is asynchronous. Let us see now how an asynchronous DHE-like part can be added to P3 to make it fully asynchronous.
X3DH
The DHE protocol allows for A and B to share a common secret s over an authenticated channel, but both parties must be online at the same time. However, in order for A to compute the shared secret s, A only needs an ephemeral public key epkB from B, along with the signature sB of epkB by the permanent secret key skB. The server that links A and B can be used to store i pre-fetched pairs (epkBi, sBi) in order for different contacts to initiate a conversation. The initialization step of the protocol P3 can then be:
B sends i pairs (epkBi, sBi) to the server and stores the corresponding eskBi on her side;
A queries the server for one of the pairs and verifies the signature;
A draws an ephemeral key pair (eskA, epkA) and performs a DHE with eskA and epkBi in order to get s;
A is then able to initiate her ratchet chains and to send encrypted messages to B, adding epkA and the signature of epkA by sA;
B gets epkA from the server, verifies sA, computes s thanks to eskBi and epkA, and is now able to decrypt the messages from A.
Even if [X3DH] is slightly different in the implemented computations of s, the seminal idea is the one exposed here. The protocol P3 is now fully asynchronous!
Keys authentication matters
One of the key notions in the previous protocols P1, P2 and P3 is the authentication of the permanent keys. This setup step is not necessary to communicate, but necessary to communicate confidentially. To authenticate a public key, one way is to verify through an authenticated channel that the fingerprint of (the public key of) a contact that appears on the user's device is the same as the one that appears on the contact's device. The usual way to perform this verification is to scan a QR code encoding the fingerprint of the targeted key.
This generally optional verification is actually mandatory to perform in Olvid.
Post-compromise security
A system provides post-compromise security (PCS) if compromising the current secrets of a user does not allow an attacker to decrypt the messages exchanged after the attack or the leak. This notion was first formalized in [CGCG16] for authenticated key-exchange.
In the protocol P1, to compute each key encrypting a message, PCS is provided, since the keys change every time and are chosen randomly (note, however, that if the private key leaks, an attacker can impersonate the victim, but cannot decrypt the encrypted messages without knowing the corresponding ephemeral secret keys).
For the protocol P2 that we use for the end-to-end encryption on Mattermost, there is no full-PCS, for the same reason as there is no full-PFS: indeed, if the permanent material of A leaks, all the messages she received or will receive may be decrypted, but not the messages she sent or will send.
We now need to examine the protocol P3, i.e. the one close to Signal. As is, our protocol does not provide PCS: that will be the goal of the double ratchet, detailed below.
- Note:
- The messaging protocol implemented in Wickr [WPW] partially provides both PFS and PCS: to simplify, Wickr uses an idea similar to PGP, and for each message sent to B, A generates a random symmetric key k and a random asymmetric key pair (pk, sk), she then computes the DH of sk and pkB (B's long-term key) and uses that value as input to a KDF (with other elements, see [WPW]), encrypting the key k with the output. Knowing k or sk for a given message would not allow an attacker to decrypt any other message, but knowing B's long-term private key(s) would mean the attacker is able to decrypt every message sent (or that will be sent) to B.
Double ratchet
Let's recap:
with one ratchet, the Signal protocol provides PFS by making the keys evolve via a one-way function,
with a (costly) DHE for each message, we have both PFS and PCS.
The hybrid solution is then to regularly perform a new DHE key exchange, simpler than X3DH, to refresh the ratchet that is used to obtain PFS by injecting some randomness: this step is the second (asymmetric) ratchet, which finally brings us to the double ratchet protocol.
The question is how regularly to perform the second ratchet: performed for every message, we go back to protocols P1/P2. If the period is too long, this could imply a large leak, since, once the attack is performed, all the messages exchanged within that period can be decrypted.
In the documentation of the double ratchet [DR], the proposition is to make a DHE every time a speaker is interrupted and wants to talk again. In a walkie-talkie communication, it ensures the same security as a DHE for every message, i.e. protocol P1.
Note that recent work by Blazy et al. [BFJLOR22] does propose to edit Signal and perform a new DHE at each step, thus sending an ephemeral public key in the additional data of every message – and signing that public key to ensure that it did come from the sender and was not injected by an attacker in order to derail the conversation (this signature makes their protocol lose the deniability property, see below). To handle lost or out-of-order messages, the sender has to add every past public key to the messages' additional data until they are acknowledged. As usual, there is a choice to be made between efficiency (and thus usability) and security.
Other properties
Deniability
A messaging protocol is said to be deniable if, given a transcript, a user can deny having participated in the conversation, no matter whether the conversation is real or not. In particular, a protocol is deniable if any user A can simulate a conversation transcript with any other user B that is indistinguishable from a legit conversation: this is doable if the protocol is such that at no point does B provide any value or information that A does not know or cannot obtain. In Signal, we reach deniability because once A receives a public key bundle from the server, she can compute any and all following key material herself: the only thing B would normally do is provide randomness for the asymmetric ratchet, but there is no way to distinguish random values generated by A from random values generated by B: she can thus play both roles.
In short, instead of achieving deniability by being able to prove that B did not participate, we achieve it by not being able to prove that B did participate in the conversation.
Note that deniability is desirable to ensure that users cannot be denounced, or tricked into producing incriminating messages.
There is sometimes a misunderstanding as to how deniability may be mixed with authenticity of the messages. We can summarize the two properties as follows:
authenticity: A wants to be sure that she is talking with B.
deniability: A wants to prove to everybody that she talked to B.
We can ensure both properties at the same time: authenticity must be proved inside the conversation, between the protagonists themselves, while deniability must be proved outside the conversation, to non-participants. Signal, for example, achieves both deniability and authenticity.
Encryption at rest
If end-to-end encryption refers to encryption on the move, it is also important to know what happens to messages once they are received, both client-side, and server-side.
- Same encryption
- One obvious option is to store them encrypted as is, i.e. A receives c=Enc(m) from B, decrypts it to read it, and the app will locally store c, fetching it and re-decrypting it as needed. However, that means that A must keep whatever key is used to decrypt c, thus losing Forward Secrecy: at any given time, the application's state would contain keys to decrypt the entire backlog.
- Re-encrypt
- Another solution is to re-encrypt the messages with another key, and store them either server-side or client-side, using the secure storage of the device: e.g. this is what Wickr does, as detailed in the Encrypted Local Storage section of their whitepaper [WPW]. In this case, the PFS may not be broken if the secure storage is really secure.
- Server-side
- We find the same options when storing the messages on the server, either using a new key or storing the messages as they are. This is the choice done for the mattermost plugin, which stores on the server both the encrypted messages for A and for B, no matter who is the sender, as opposed to what is described for P2 (which is only partly PFS). Therefore, even if the mattermost plugin provides end-to-end encryption, it does not provide PFS or PCS.
Post-quantum security
As seen previously, we can divide the complete Signal protocol in different steps:
the initial session key exchange (X3DH);
the (symmetric) ratchet steps to provide PFS;
the (asymmetric) ratchet step to provide PCS;
the (symmetric) ratchet steps to provide PFS;
the (asymmetric) ratchet step to provide PCS;
...
In the previous enumeration, the even (symmetric) steps are already quantum-safe; doubling the size of the key is often sufficient to be quantum-safe if the key size is small (from a quantum-safe standard).
However, the odd (asymmetric) steps, relying on (some sort of) Diffie–Hellman–Merkle protocols, are not quantum-safe. The most important one is the first step of the protocol: indeed, achieving PCS is done by classical DHE, which is not a particularity of the Signal protocol and is thus studied independently. This is, however, not a simple problem to solve, but the X3DH one is more important to discuss here.
Building an X3DH-like post-quantum protocol is not that easy. It is needed to reach all the security goals of X3DH, which are not fully formalized and established. In addition, the diversity of propositions for quantum-safe key-establishment algorithms is wide: at least
4 finalists for Post-Quantum Cryptography Standardization: 3 lattice-based and 1 code-based systems;
5 alternate candidates: 1 isogeny-based, 2 lattice-based and 1 code-based systems;
CSIDH, which is an isogeny-based system.
We refer to our blog post about post-quantum cryptography for more details about the development of the post-quantum cryptography and the challenges implied.
Some articles, like [BFGJS19], [HKKP21], [BFGJS21] and [DG21] address the problem of having an X3DH-like post-quantum secure system. Compared to the classical X3DH, all of these schemes cannot completely mimic what X3DH provides (see Page 3 of [DG21] for a comparison). All require additional data to be exchanged (proofs of knowledge, ciphertexts prior to the classical encrypted messages, etc.) or different security assumptions: this shows that plugging new key exchange mechanisms to replace the Diffie–Hellman–Merkle one is not that easy and needs to be done carefully!
These Signal-like protocols are not only a theoretical problem. If solving the protocol issue is yet a big deal, having an efficient implementation of a (reduced) version of these protocols is another issue! Indeed, post-quantum cryptography for key exchange mechanisms is known to require more bandwidth to share the data and often more computational power than the classical ECDH.
The efficiency challenge is highlighted for group conversation, both in classical cryptography and in post-quantum cryptography. In the second part of the blogpost, we will detail how to achieve group conversation in multiple models, trying to always reduce the bandwidth without sacrificing the security and the user-friendliness.
Acknowledgments
These articles are inspired from a talk we gave at Quarkslab's Quarks in the Shell event in 2021 with Marion and Charlie, and we thank both of them for the many discussions we had for the preparation of this talk. We also thank Adrien and Philippe for the helpful reviews.
Bibliography
| [BCSJNS17] | "Ratcheted Encryption and Key Exchange: The Security of Messaging" M. Bellare, A. Camper Singh, J. Jaeger, M. Nyayapati and I. Stepanovs. https://eprint.iacr.org/2016/1028 |
| [BFGJS19] | "Towards Post-Quantum Security for Signal's X3DH Handshake", J. Brendel, M. Fischlin, F. Günther, C. Janson and D. Stebila, SAC 2020. https://eprint.iacr.org/2019/1356 |
| [BFGJS21] | "Post-quantum Asynchronous Deniable Key Exchange and the Signal Handshake" J. Brendel, R. Fiedler, F. Günther, C. Janson and D. Stebila, 4 August 2021. https://eprint.iacr.org/2021/769 |
| [BFJLOR22] | "MARSHAL: Messaging with Asynchronous Ratchets and Signatures for faster HeALing" O. Blazy, P.-A. Fouque, T. Jacques, P. Lafourcade, C. Onete and L. Robert. https://hal.uca.fr/hal-03510612/document |
| [BS20] | "Security under Message-Derived Keys: Signcryption in iMessage", M. Bellare and I. Stepanovs. https://eprint.iacr.org/2020/224 |
| [CFKN20] | "Clone Detection in Secure Messaging:Improving Post-Compromise Security in Practice", C. Cremers, J. Fairoze, B. Kiesl and A. Naska. https://people.cispa.io/cas.cremers/downloads/papers/CFKN2020-messaging_cloning.pdf |
| [CGC17] | "Mind the Gap: Where Provable Security and Real-World Messaging Don't Quite Meet" K. Cohn-Gordon and C. Cremers. https://eprint.iacr.org/2017/982 |
| [CGCG16] | "Post-Compromise Security" K. Cohn-Gordon, C. Cremers and L. Garratt. https://eprint.iacr.org/2016/221 |
| [CGCDGS16] | "A Formal Security Analysis of the Signal Messaging Protocol", K. Cohn-Gordon, C. Cremers, B. Dowling, L. Garratt and D. Stebila https://eprint.iacr.org/2016/1013 |
| [DG21] | (1, 2) "Post-Quantum Signal Key Agreement with SIDH", S. Dobson and S. Galbraith, 20 September 2021. https://eprint.iacr.org/2021/1187 |
| [DH76] | "New Directions in Cryptography", W. Diffie and M. Hellman, IEEE Transactions on Information Theory. https://ee.stanford.edu/%7Ehellman/publications/24.pdf |
| [DvOW92] | "Authentication and Authenticated Key Exchanges", W. Diffie, P. van Oorschot and M. Wiener, Designs, Codes and Cryptography. https://people.scs.carleton.ca/~paulv/papers/sts-final.pdf |
| [DR] | (1, 2) "The Double Ratchet Algorithm", T. Perrin and M. Marlinspike. https://signal.org/docs/specifications/doubleratchet/ |
| [Hel02] | "An overview of public key cryptography", M. Hellman, IEEE Communications Magazine. https://www-ee.stanford.edu/~hellman/publications/31.pdf |
| [HKKP21] | "An Efficient and Generic Construction for Signal's Handshake (X3DH): Post-Quantum, State Leakage Secure, and Deniable", K. Hashimoto, S. Katsumata, K. Kwiatkowski and T. Prest, PKC 2021. https://eprint.iacr.org/2021/616 |
| [KBB17] | "Automated Verification for Secure Messaging Protocols and their Implementations: A Symbolic and Computational Approach" N. Kobeissi, K. Bhargavan and B. Blanchet https://bblanche.gitlabpages.inria.fr/publications/KobeissiBhargavanBlanchetEuroSP17.pdf |
| [WPW] | (1, 2, 3) "Wickr Messaging Protocol" https://wickr.com/wp-content/uploads/2019/12/WhitePaper_WickrMessagingProtocol.pdf |
| [X3DH] | "The X3DH Key Agreement Protocol", M. Marlinspike and T. Perrin. https://signal.org/docs/specifications/x3dh/ |