Post-quantum cryptography is an active field of research, especially since the NIST Call for Submissions in 2016 to design new standards for asymmetric key cryptography. The aim of post-quantum cryptography is to mitigate the risk of a large-scale quantum computer which may break all the asymmetric cryptography that is deployed today. This blogpost will present the activity state of the post-quantum cryptography field and sketch the challenges for the deployment of post-quantum safe standards for the industry, both in term of internal infrastructures and security products.
At the occasion of the workshop "Mise en œuvre de la cryptographie post-quantique" (Implementing post-quantum cryptography) hosted at the European Cyber Week, some interesting point-of-views, recommendations and state-of-the-art talks were given. This is a starting point for us to gather the up-to-date information. Among all the talks of the workshop, three of them were already given in a preliminary version on the 23rd of April 2021 at the "Journée mise en œuvre d'implémentation de cryptographie post-quantique": the slides may be downloaded on the SemSecuElec page.
Introduction
Post-quantum cryptography is a new set of cryptographic primitives. However, today's cryptography usage is not only made of primitives, it is a more complex architecture. At Quarkslab, we formalized cryptography as the following stack:
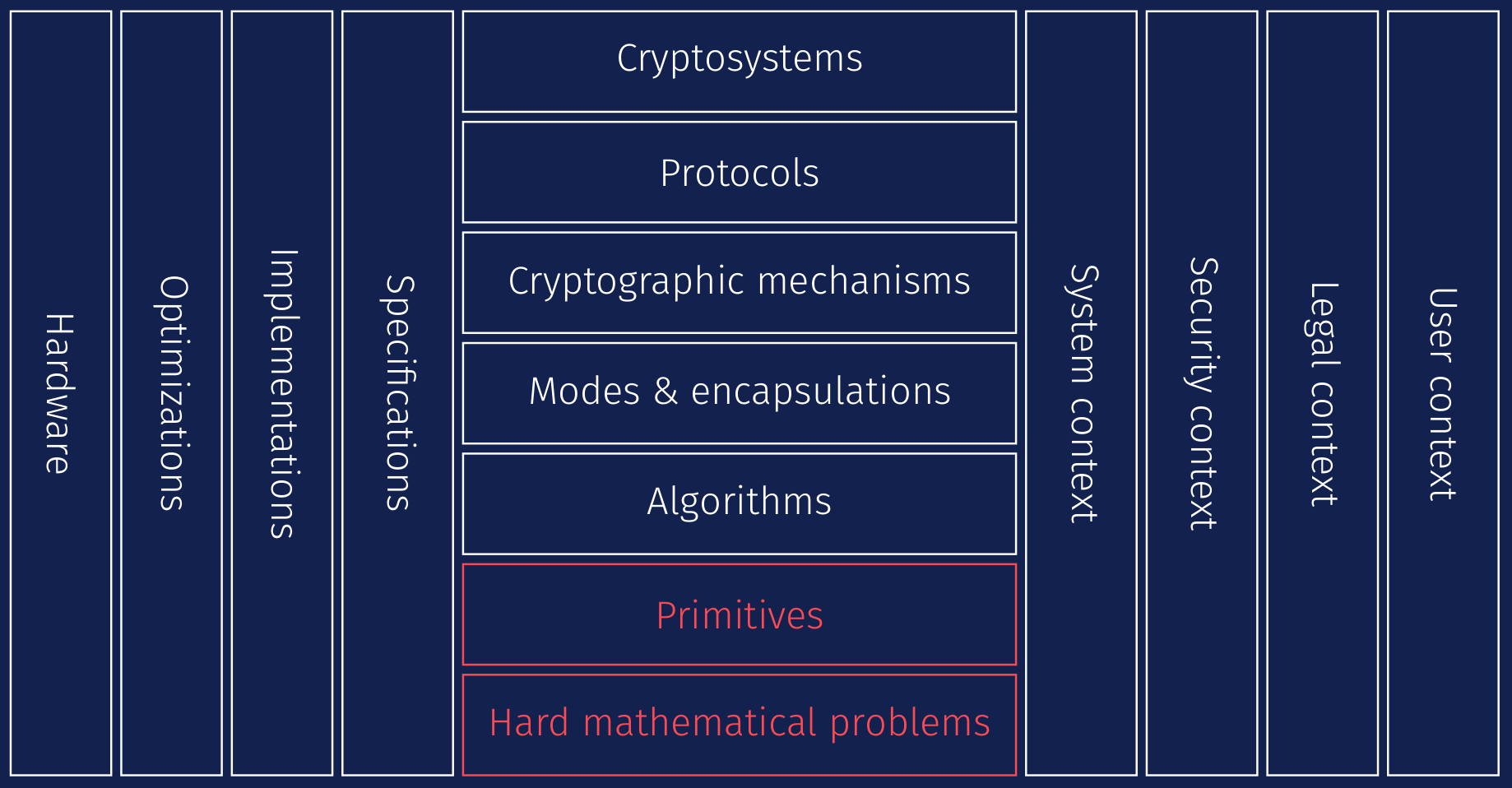
On hard mathematical problems, such as factorization, cryptographers built primitives, let us say the textbook RSA. Algorithms are then built to give algorithmic details, for example how to perform modular exponentiations or how to avoid weak keys. Then, modes or encapsulations define a real message processing, as in RSA-OAEP [RFC8017]. The encrypted messages are part of a cryptographic mechanism which defines among other the encoding of the inputs and outputs, and this mechanism is part of protocols, TLS for example. At the top of our stack stays the cryptosystem, which gathers several protocols, as OpenSSL or MbedTLS may provide. They are also one of the main components to allow the calls to the OS internals and the support of various microarchitectures, which are dependent of the system designs. The legal context may restrict some usage, because of patents or constraints to security parameters, which impact the security context an organization may deploy on their infrastructures. To better take into account all the best implementation practices, a specification work is needed. Ultimately, the standard is deployed in a variety of systems (from smartcard to server), requiring sometimes hardware optimizations to address physical constraints (memory, efficiency, etc.).
The example we gave with RSA can also be done with AES where:
inverting AES is the hard mathematical problem;
AES is the primitive;
arithmetic in finite fields of characteristic two is a component of the algorithm details;
AES-GCM is a mode.
Post-quantum cryptography is a set of new primitives built upon hard mathematical problems (the red part of our stack). These asymmetric primitives are supposed to remain secure against a quantum computer, and a replacement to the classical asymmetric primitives. However, one can understand that this is not as simple as plug-and-play from a primitive to another. One may hope that at the cryptographic mechanism level, a classical mechanism will be replaced by a post-quantum one. In the following sections, we will describe the risk a large-scale quantum computer represents against the cryptography that is deployed today, what are the solutions to mitigate the risk and how to shift from today's cryptography to post-quantum cryptography in the smoothest way.
The end is near?
First, we can ask ourselves how realistic is the fear about the emergence of a possible large scale quantum computer on cryptography.
Quantum computer is coming
Classical computers act on bits, which is the basic unit of information to store data. To run an algorithm, you need enough memory: for example, factoring large numbers with the Number Field Sieve (NFS) algorithm [NFS] requires at a point to store about 1.5 TB of data [BGGHT].
The equivalent notion for a quantum computer is the qubit. Storing information on qubits provides some benefits for computations, but it is a difficult task, with physical, chemical and engineering challenges, such as dealing with close to absolute zero elementary particles. Note that the algorithmic speed-ups coming from a quantum computer described in the next section are not because quantum computers are sort of supercomputers under steroids, but because quantum computers compute in a completely different way than classical computers. An interested reader may refer to Institute for Quantum Computing for more information.
However, as in classical computers, the size of quantum computers matters to understand which type of quantum algorithm may be launched, and on which data. Recently, researchers of different companies or universities reached 49 qubits with the Intel "Tangle Lake" and even 72 qubits with the Google "Bristlecone" in 2018, 76 qubits with the University of Science and Technology of China "Jiuzhang" in 2020 and 127 qubits with the IBM "Eagle" this year. Despite not being exhaustive, this small list shows the intense activity in this field, and the IBM roadmap for the coming years lets us expect new advances.
Impact on cryptography
For now, the size of the quantum computers is well suited to give some accelerations for simulations in natural sciences. However, our particular interest in this blogpost is the impact of a quantum computer for cryptography and security aspects.
Quantum computer threat
Among numerous quantum algorithms, two of them matter directly for today's cryptography: Shor's algorithm [Shor] and Grover's algorithm [Grover]. Shor's algorithm has direct applications on solving the discrete logarithm problem (DLP), both on finite fields or on elliptic curve, and on factorization: the algorithm is cubic in the bit size of the element to factor ( with this bit size), when the NFS algorithm is sub-exponential.
Grover's one impacts the security of symmetric key cryptography: on unstructured search on a black box function, a classical algorithm will require at worst the evaluation of the function on all the input range, while the quantum algorithm will only need to evaluate on square root elements of the input range. The complexities are summarized in the following table:
Then, to mitigate a large-scale quantum computer, at a classical security level, doubling the size of symmetric keys is sufficient to ensure the security level in a quantum world. However, asymmetric cryptography needs to rely on new paradigms than the ones deployed today.
Quantum computer sizes
If Shor's algorithm is really devastating in destroying classical asymmetric cryptography, we have not yet spoken about the qubits requirement of the algorithm. Using Table 2 of [GE], we can see that, in 2012, 1,000,000,000 qubits were expected to be needed in order to perform the algorithm; that number plummets to 230,000,000 in 2017, then to 170,000,000 and 16,000,000 in 2019, and finally goes down to 13,436 according to [GS]: these improvements come from both algorithmic progresses and new developments in quantum computer architectures. We then find ourselves in a situation where the required qubits to factor a large number decreases when the number of physical qubits in a real quantum computer increases. There is nevertheless a gap between the number of logical qubits (how many qubits are needed to perform an algorithm) and physical qubits (how many qubits are present in a quantum computer): indeed, a logical qubit may need more physical qubits to be represented. However, this does not change the trend of the analysis. See [GM] for more information.
Another approach [BBM] is to use a quantum computer as an accelerator for some steps of the NFS algorithm to factor large numbers. It will asymptotically require less qubits (a sub-linear number while Shor's algorithm requires a linear number) than factorization on a quantum computer using Shor's algorithm, but the algorithm stays in the sub-exponential category, with 1.387 instead of 1.923 for the complexity. The interested reader may have a look at the BSI report on the development of a quantum computer and its impacts [BSIQC].
If we agree on the need to switch to new cryptographic algorithms to mitigate the quantum computer threat, when do we need to act?
ETA WEN
The question "when should we worry?" is a bit more complex than it sounds. In 2015, M. Mosca in [Mos15] states:
estimate(s) a 1/7 chance of breaking RSA-2048 by 2026 and a 1/2 chance by 2031.
In this article, M. Mosca explains the key elements for this estimation:
When will we reach the design of a fault-tolerant scalable qubit?
How many physical qubits will we need to break RSA-2048?
How long will it take to scale the scalable design to the size sufficient to break RSA-2048?
A more recent study [MP] confirms this estimation, since a bit more than half of 44 experts expect with more than 1/2 the possibility of having a crytographic-threat quantum computer around 2035.
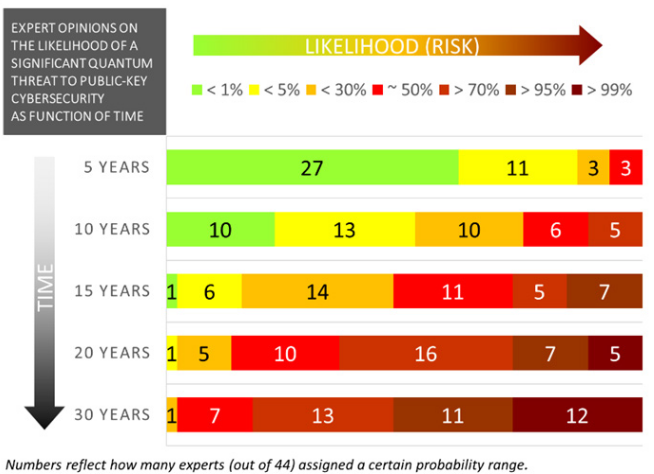44 expert opinions on the possibility to have a large-scale quantum computer
(extracted from [MP]_, publish in January 2021).We then have a date for the quantum cryptocalypse: around 2035. But is that sufficient?
A well known element for planning the transition is the Mosca's theorem [Mos13] (page 42), depicted in the following picture, where y is the time needed to have post-quantum cryptography standards deployed, x is the time the data need to be kept secret or signed, and z is the time to build a large-scale quantum computer:
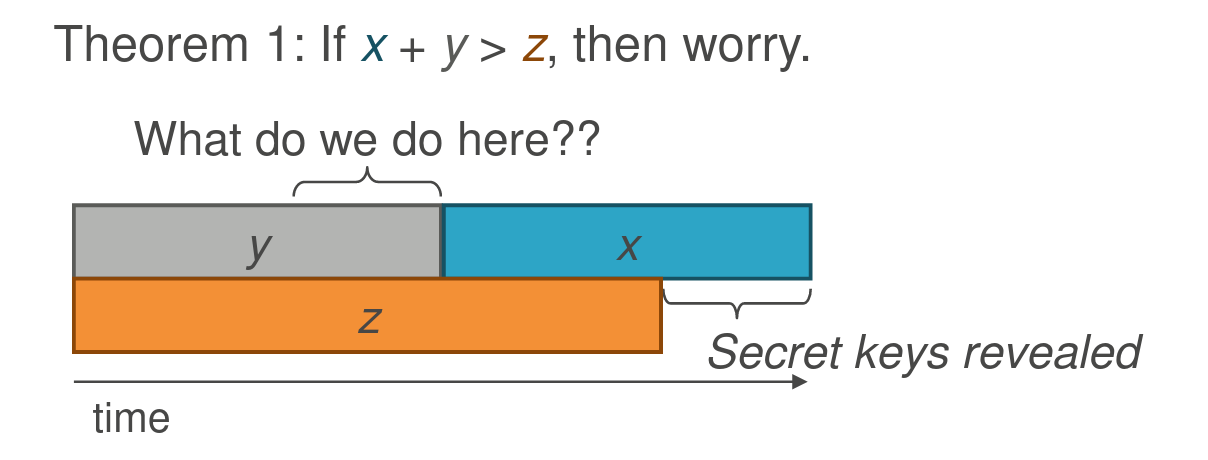Mosca's theorem (`source Then, the end is not 2035, but 2035 - time limit to standardize - time limit to keep the data secret. According to the NIST [Mod],
The 3rd Round will end sometime close to the end of 2021.
We expect to release draft standards for public comment in 2022-2023.
The first set of standards will hopefully be finalized by 2024.
Let us consider a TLS exchange. A first step is to agree thanks to the Diffie–Hellman (DH) key exchange on a common shared secret, using asymmetric cryptography, in order to use symmetric cryptography with this shared secret to encrypt messages. If the security choices are conservative, the DH key exchange will be done, for example, on elliptic curve over the NIST P-521 and the symmetric cryptography algorithm will be AES256-GCM. A well known security feature of DH key exchange is perfect forward secrecy when using ephemeral keys, which ensures that, if at some point, all the cryptographic material leaks, the messages exchanged before the leak remain confidential. Let us suppose now that we have access to a large-scale quantum computer: the symmetrically encrypted messages are still confidential, since we have large symmetric keys. However, the initialization of the TLS exchange with DH is completely insecure. Then, the shared secret can be recovered, and with that, all the keys used to symmetrically encrypt messages. Note that this problem is the same with PGP encrypted messages, Whatsapp / Signal messages and so many other applications.
In a classical world, neither of DH nor Enc (symmetric encryption) may be
recovered in a TLS session. In a quantum world, Enc cannot be broken per se,
but since DH can be, the key used in Enc is consequently broken.For signatures, the problem is a bit different and seems less urgent. The threat of an attacker having a quantum computer is to impersonate someone and forge signatures. However, long-term chains of trust should take steps now to mitigate the threat and prepare transition processes.
Then, if we assume that all of us will migrate to the post-quantum cryptography standards once published, the confidential data you exchanged NOW (through TLS for example) must not be sensitive in 10 years. This is a huge problem! Migrating all our cryptography from classical to post-quantum cryptography mechanisms will be a long journey and we are all going on an adventure! This challenge is one of the most important regarding deployment of cryptography. Maybe, cryptocalypse will not just be the large-scale quantum computer, but only the transition by itself. Let us see how we can try to be the most efficient in the remaining time.
Migration
Some reminders
Migrating to new systems is hard. And the history of (cryptographic) transitions to new standards is not quiet and easy: as we all know that adoption of new standards or new software equipments is often done lazily. We have some examples:
the use of deprecated primitives, such as RC4, see SSL Labs RC4 Deprecation Plan, or more recently SHA-1 [WYY] [SBKAM];
the use of deprecated cryptographic parameters, for example [FREAK] and [Logjam];
and so many other misuses.
Sometimes, a shift to a new standard is stopped in order to wait for new (expected to be safer) standards [KM]: crypto agility may be a good option to not delay adoption of standards, even for a short period of time.
We know that shifting is hard, and believing that a NIST standard or a RFC will be applied once officially approved may take way more time to be adopted. Then, the Mosca's theorem is way more problematic than the 10 years we emphasized in the last section. If we know that adoption of a standard is difficult, we need to know what we need to shift for.
What to standardize
At the beginning of 2016, NIST announced the opening of a Call for Submissions [PQCCS] in order to design one or more new standards for post-quantum asymmetric key cryptography. Indeed, the standards [SP80056A], [SP80056B] and [FIPS186] are all vulnerable to the quantum computer threat, since they rely on classical asymmetric cryptography. There were 69 candidates for the first round, among which we can distinguish 5 scheme categories (based on different hard mathematical problems) that are still present in the last round of the process:
lattice (structured and unstructured) based;
code based;
multivariate based;
one-way function / hash based (for signature only);
isogeny based.
An interested reader may refer to Post-Quantum Cryptography Lounge or PQC wiki for more information about the candidates (4 key encapsulation mechanism finalists and 5 alternate candidates, 3 signature finalists and 3 alternate candidates), and obviously the NIST PQC website. An introduction to the foundations of these schemes may be found in [HPA]. ESTI technical reports on NIST round-3 post-quantum schemes about key encapsulation mechanisms [QSPKE] and signatures [QSS] are interesting compendiums.
One of the challenges is to design a candidate which:
is resistant to classical and quantum attacks;
has good performances (time, memory, etc.);
is compatible with existing protocols (perfect forward secrecy, etc.);
is side-channel resistant;
reaches a good level of security.
There are five different level of security, the levels 1, 3, and 5 correspond to a resistance comparable to the exhaustive search to break respectively AES-128, AES-192 and AES-256, while the levels 2 and 4 correspond to the difficulty to find a collision on SHA-256 or SHA-384. More information about the selection criteria may be found in Submission Requirements and Evaluation Criteria for the Post-Quantum Cryptography Standardization Process. We can understand that, with all these requirements, taking decisions for the standard is not that easy!
At this point, you may acknowledge that we need to shift to new standards soon, that there are many options to replace asymmetric cryptography primitives, and you may ask to what we need to change. If these questions are important, we need to describe how to make the change in the most agile way. Indeed, for some parameters or algorithms,
the maturity level of the post-quantum algorithms (is almost) the maturity level of RSA in the mid 90's. [Ros]
Hardcoding a choice now would lead to difficulties in the future.
How to shift (the French example)
The ANSSI (Agence Nationale de la Sécurité des Systèmes d’Information, French National Agency for the Security of Information Systems) regularly publishes guides and whitepapers about security and cryptography practices. In one of the last documents about the choice of cryptographic algorithms [ANSSI], the ANSSI recommends that, for information which must remain protected after 2030, the hybridation mechanism may be used [SP80056C]. Hybridation is the use of both a classical and a post-quantum primitives in order to derive keys (combining both of the shared secrets) or to sign documents. Indeed the ANSSI does not suggest to jump directly from classical to post-quantum cryptography, except for hash-based signatures. This is in line with the french "Plan quantique".
In the PQCrypto 2021 conference, the ANSSI shared its views on the post-quantum cryptography transition [Ros]. The agency proposes a three phases transition:
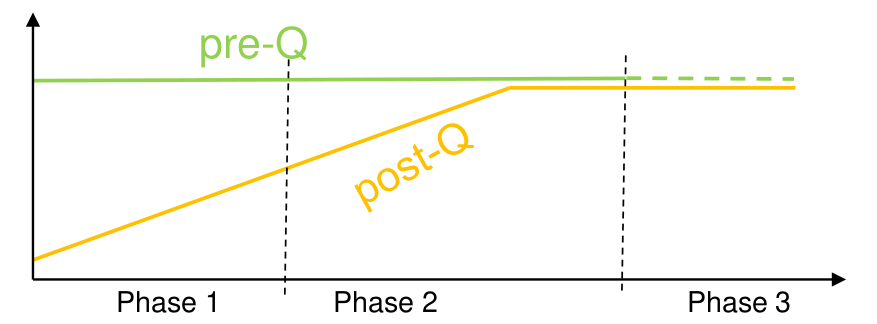Three steps post-quantum cryptography transition (extracted from [Ros]_). The
horizontal axis is the time, the vertical one is the deployement level, pre-Q
stands for classical (pre-quantum) cryptography and post-Q stands for
post-quantum cryptography.In step 1, in which we actually are, hybridation is only recommended. The main goal of this step is to avoid security regression. There will be no obligation to use a precise post-quantum algorithm, but good choices are:
a finalist or alternate scheme of the NIST round 3 standardization process;
the use of level V parameters.
If such a choice is made, the symmetric cryptography parameters must also be increased to 256 bits of classical security.
In step 2, hybridation is mandatory for all security products. A list of acceptable algorithms will be provided, which may include more (or less) algorithms than the NIST standards. FrodoKEM, for example, seems a good candidate if NIST does not standardize it.
In step 3, hybridation becomes optional, in the sense that post-quantum algorithms are mandatory, but classical asymmetric cryptography is no longer a prerequisite.
The precise timeline will be announced in the following weeks by the ANSSI. With maybe another timeline, BSI in [BSITG] shares the same findings as the ANSSI about hybridation and FrodoKEM. As you may remark, choice of algorithms, and maybe parameters, may not be completely specified even if the transition is asked for. The transition must therefore be smooth and atomically performed, keeping in mind the fact that things may evolve quickly.
Crypto agility
Moving to post-quantum cryptography is something that may need multiple iterations, especially if the transition is started quickly. Even if post-quantum cryptography may be plugged-and-played as a replacement of classical cryptography (which is not completely sure), a complete inventory of the data and how they are (cryptographically) protected seems mandatory. This may start by:
discovering and classifying data;
making an inventory of the cryptography (primitives, modes, key size, parameters, security models, etc.);
engaging into a crypto agility process;
looping on the process to be up-to-date regularly.
Ultimately, the crypto agility process will help to quickly update cryptographic primitives, either because the standard evolves, the cryptographic primitives are broken or deprecated, or whatever reason which implies a transition. This long process may at some point be close to automatic, which implies numerous tooling and software problems to be solved. The road to a quantum-safe world may be at this cost.
An effort is also done by organizations to gather transition recommendations. Among others, we can note:
NIST on transition of cryptographic algorithms and key lengths [SP800131A];
the document "A Methodology for Quantum Risk Assessment" [MM];
the document "Getting Ready for Post-Quantum Cryptography" [BPS].
We are now ready for the last part of the blog post, describing what to follow for the standardization processes.
From standardization to implementation
Standardization and evaluation
First standardized post-quantum cryptographic primitives are the stateful hash-based signature schemes in [RFC8391], [RFC8554] and [SP800208]. However, these schemes
are not suitable for general use because they require careful state management that is often difficult to assure. [SP800208]
In order to have more generic primitives, the result of the round 3 will be soon announced, and, according to the Third Round Candidate Announcement
NIST intends to select, at most, one (structured lattice scheme) for the standard.
The other schemes will be evaluated individually, whatever their paradigm. Note also that patent issues (also subject to debate) may slow down the process, see [LS] or Fighting patents. Another round is planned to open to new schemes (except structured lattices) or schemes already in the competition for which it is needed to have more confidence before adoption.
Other efforts to standardize and assess post-quantum cryptography are running, such as:
NSA plans to add in the Commercial National Security Algorithm Suite lattice-based and stateful hash-based signatures, according to Quantum Computing and Post-Quantum Cryptography FAQs;
RFC drafts [KEM], [MPKAC], [PQCC], [PQCK], [PQCS], [PQECK] [PQTLS12], [PQTLS13] and [PQSSH] for example;
consortiums of academic and industrial entities, such as Open Quantum Safe, Safecrypto, PQCRYPTO, PROMETHEUS, RISQ.
These consortiums are involved both in the proposition process (submissions, reviews, assessments, etc.) and in practical deployments of post-quantum cryptography in real life applications.
Benchmarks and applications
In the variety of cryptographic post-quantum submissions, there are many differences between types of schemes and their implementations. For example, lattice based schemes have an equivalent size for public key and signature, whereas hash-based signature schemes have a tiny public key (around 64-byte length for level V security) but large signatures (29792-byte length for SPHINCS+-small according to the documentation).
With all the size and performance parameters, it is possible to find a post-quantum primitive that fits into some of the constraints, especially for constraints on personal computers. For more details about performances and choices of primitives, we refer for example to SUPERCOP, The TLS Post-Quantum Experiment, Sizing Up Post-Quantum Signatures or [PST]. Other considerations may also take into account the ability to provide ephemeral or static key encapsulation mechanisms.
If software code is provided and extensively investigated in the NIST review process, hardware acceleration, through FPGA and ASIC, is also considered by researchers in order to compete with the performances of classical cryptographic primitives, see [CHKSSY]. In some context, side-channel resistance needs also to be part of the consideration, see [KFTNAH] for example. Reaching all the goals (side-channel resistance, efficiency, sizes, etc.) at the same time is a difficult task and needs to be thought in advance. For example, Mitaka [Mitaka] is a new scheme based on Falcon (structured lattice-based submission in the round 3 of the NIST standardization) which is thought to be masked (and then resistant to some side-channel attacks) by design. About small devices (typically IoT or smartcards), post-quantum cryptography deployment is not that easy either, in particular due to the memory constraint, see [PQM4], [Gre] and [KP].
Implementations and applications
Once a quantum-safe primitive is chosen, taking into consideration all the constraints we listed previously, it is necessary to find the convenient implementation. As far as we know, there exists two types of post-quantum cryptography libraries:
open source, such as liboqs and PQClean, which are not aimed to be used in production, see the README.md of liboqs for example;
closed source, which are for now not evaluated nor certified by third-party entities.
Note that some open source libraries or software already propose post-quantum safe primitives, as strongSwan with BLISS or OpenSSH 8 with Streamlined NTRU Prime. The use of these implementations must be done with care:
about the attacker model, being immune to side-channel attacks is not always ensured, as shown in [TW] for BLISS;
about the configuration parameters, subject to modification, as the replacement of sntrup4591761x25519-sha512@tinyssh.org by sntrup761x25519-sha512@openssh.com in OpenSSH 8.5.
This is however no good reason to run experiments on non-critical infrastructures: for example, the Open Quantum Safe (OQS) openssl, the OQS boringssl and the OQS openssh, which are at an experimental stage, may be used for prototyping deployments of post-quantum safe cryptography. On top of closed source libraries, companies sell different products, such as VPNs or secure messaging applications.
Conclusion
Post-quantum cryptography deployment is a challenge for all the organizations. Numerous solutions are already practicable to shift from classical to post-quantum cryptography, but waiting for a large-scale quantum computer to shift is not the good option to ensure security of long term data. Assessing the implementations of the new post-quantum safe software or libraries will also be an intense challenge.
This blogpost proposes a long bibliography, which is however very poor compared to the extensive literature on the post-quantum cryptography subject. If you want to explore or to have more details on some subject, you will find a lot of valuable references and may learn a lot of new techniques. Have a nice journey discovering this stimulating field!
Acknowledgments
We want to thank first all the organizers and speakers for such a high-quality workshop. We want also to thank all the participants for the nice and interesting side discussions. We wait impatiently for a possible second edition of this workshop. We thank Adrien, Angèle, Francisco, Fred, Mahé, Marion and Robin for their feedback on this blogpost.
Bibliography
| [ANSSI] | Guide de sélection d’algorithmes cryptographiques, Guide ANSSI, version 1.0, 8 March 2021. https://www.ssi.gouv.fr/uploads/2021/03/anssi-guide-selection_crypto-1.0.pdf |
| [BBM] | A low-resource quantum factoring algorithm, D. J. Bernstein, J.-F. Biasse and M. Mosca, PQCrypto 2017. https://eprint.iacr.org/2017/352 |
| [BGGHT] | Comparing the Difficulty of Factorization and Discrete Logarithm: A 240-Digit Experiment, F. Boudot, P. Gaudry, A. Guillevic, N. Heninger, E. Thomé and P. Zimmermann, CRYPTO 2020. https://eprint.iacr.org/2020/697 |
| [BPS] | Getting Ready for Post-Quantum Cryptography: Exploring Challenges Associated with Adopting and Using Post-Quantum Cryptographic Algorithms, W. Barker, W. Polk and M. Souppaya, NIST Cybersecurity White Paper, 28 April 2021. https://doi.org/10.6028/NIST.CSWP.04282021 |
| [BSITG] | Cryptographic Mechanisms: Recommendations and Key Lengths, BSI, Technical Guideline, 24 March 2021. https://www.bsi.bund.de/SharedDocs/Downloads/EN/BSI/Publications/TechGuidelines/TG02102/BSI-TR-02102-1.pdf?__blob=publicationFile |
| [BSIQC] | Status of quantum computer development, BSI, version 1.2, June 2020. https://www.bsi.bund.de/EN/Topics/Cryptography/QuantumComputing/quantum_computing.html |
| [CHKSSY] | NTT Multiplication for NTT-unfriendly Rings, C.-M. Marvin Chung, V. Hwang, M. J. Kannwischer, G. Seiler, C.-J. Shih and B.-Y. Yang, CHES 2021. https://eprint.iacr.org/2020/1397 |
| [FIPS186] | Digital Signature Standard (DSS), NIST, Federal Information Processing Standards Publication 186-4, July 2013. https://doi.org/10.6028/NIST.FIPS.186-4 |
| [FREAK] | https://freakattack.com/, 3 March 2015. |
| [GE] | How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits, C. Gidney and M. Ekerå, Quantum 5, 433 (2021). https://arxiv.org/abs/1905.09749 |
| [GM] | A Resource Estimation Framework For Quantum Attacks Against Cryptographic Functions: Recent Developments, V. Gheorghiu and M. Mosca, March 2021. https://globalriskinstitute.org/wp-content/uploads/2021/03/2021-03-MOSCA-Quantum-Risk-February-Report-V2.pdf |
| [Gre] | Smartcard and Post-Quantum Crypto, Aurélien Greuet, NIST 3rd PQC Standardization Conference, 2021. https://csrc.nist.gov/CSRC/media/Presentations/smartcard-and-post-quantum-crypto/images-media/session-5-greuet-smartcard-pqc.pdf |
| [Grover] | A fast quantum mechanical algorithm for database search, L. K. Grover, STOC 1996. https://arxiv.org/abs/quant-ph/9605043 |
| [GS] | Factoring 2 048-bit RSA Integers in 177 Days with 13 436 Qubits and a Multimode Memory, É. Gouzien and N. Sangouard, Phys. Rev. Lett. 127, 140503 (2021). https://arxiv.org/abs/2103.06159 |
| [HPA] | SoK: How (not) to Design and Implement Post-Quantum Cryptography, J. Howe, T. Prest and D. Apon, CT-RSA 2021. https://eprint.iacr.org/2021/462 |
| [KFTNAH] | Power-based Side Channel Attack Analysis on PQC Algorithms, T. Kamucheka, M. Fahr, T. Teague, A. Nelson, D. Andrews and M. Huang, NIST 3rd PQC Standardization Conference, 2021. https://csrc.nist.gov/CSRC/media/Events/third-pqc-standardization-conference/documents/accepted-papers/kamucheka-power-based-pqc2021.pdf |
| [KP] | pqm4: NISTPQC Round 3 Results on the Cortex-M4, M. J. Kannwischer and R. Petri, NIST 3rd PQC Standardization Conference, 2021. https://csrc.nist.gov/CSRC/media/Presentations/pqm4-nistpqc-round-3-results-on-the-cortex-m4/images-media/session-3-kannwischer-pqm4.pdf |
| [Logjam] | Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice D. Adrian, K. Bhargavan, Z. Durumeric, P. Gaudry, M. Green, J. A. Halderman, N. Heninger, D. Springall, E. Thomé, L. Valenta, B. VanderSloot, E. Wustrow, S. Zanella-Béguelin and P. Zimmermann, CCS 2015. https://weakdh.org/imperfect-forward-secrecy-ccs15.pdf |
| [KEM] | KEM-based Authentication for TLS 1.3, S. Celi, P. Schwabe, D. Stebila, N. Sullivan and T. Wiggers, 12 July 2021. https://www.ietf.org/id/draft-celi-wiggers-tls-authkem-00.html |
| [KM] | A Riddle Wrapped in an Enigma, N. Koblitz and A. J. Menezes, 19 May 2018. https://eprint.iacr.org/2015/1018 |
| [LS] | Non-applicability of the Gaborit&Aguilar-Melchor patent to Kyber and Saber, V. Lyubashevsky and D. Stehlé, 8 October 2021. https://github.com/VadimLyubash/non-app-KyberSaber/blob/main/non-app.pdf |
| [Mitaka] | Mitaka: a simpler, parallelizable, maskable variant of Falcon, T. Espitau, P.-A. Fouque, F. Gérard, M. Rossi, A. Takahashi, M. Tibouchi, A. Wallet and Y. Yu, 9 November 2021. https://eprint.iacr.org/2021/1486 |
| [MM] | A Methodology for Quantum Risk Assessment, M. Mosca and J. Mulholland, 5 January 2017. https://globalriskinstitute.org/publications/3423-2/ |
| [Mod] | The Homestretch: the beginning of the end of the NIST PQC 3rd Round, D. Moody, PQCrypto 2021. http://pqcrypto2021.kr/download/program/2.2_PQCrypto2021.pdf |
| [Mos13] | Setting the Scene for the ETSI Quantum-safe Cryptography Workshop, M. Mosca, 1st Quantum-Safe-Crypto Workshop, Sophia Antipolis, 2013. https://docbox.etsi.org/workshop/2013/201309_crypto/e-proceedings_crypto_2013.pdf |
| [Mos15] | Cybersecurity in an era with quantum computers: will we be ready?, M. Mosca, 5 November 2015. https://eprint.iacr.org/2015/1075 |
| [MP] | Quantum Threat Timeline Report 2020, M. Mosca and M. Piani, 27 January 2021. https://globalriskinstitute.org/publications/quantum-threat-timeline-report-2020/ |
| [MPKAC] | Multiple Public-Key Algorithm X.509 Certificates, A. Truskovsky, D. Van Geest, S. Fluhrer, P. Kampanakis, M. Ounsworth and S. Mister, 29 August 2018. https://datatracker.ietf.org/doc/html/draft-truskovsky-lamps-pq-hybrid-x509-01 |
| [NFS] | The development of the number field sieve, A. K. Lenstra and H. W. Lenstra, 1993. https://doi.org/10.1007/BFb0091534 |
| [PQCC] | Composite Encryption For Use In Internet PKI, M. Ounsworth, J. Gray and S. Mister, Internet-Draft, 12 July 2021. https://datatracker.ietf.org/doc/html/draft-ounsworth-pq-composite-encryption-00 |
| [PQCCS] | Post-Quantum Cryptography: NIST's Plan for the Future, D. Moody, 2016. https://csrc.nist.gov/CSRC/media/Projects/Post-Quantum-Cryptography/documents/pqcrypto-2016-presentation.pdf |
| [PQCK] | Composite Public and Private Keys For Use In Internet PKI, M. Ounsworth and M. Pala, Internet-Draft, 12 July 2021. https://datatracker.ietf.org/doc/html/draft-ounsworth-pq-composite-keys-00 |
| [PQCS] | Composite Signatures For Use In Internet PKI, M. Ounsworth and M. Pala, Internet-Draft, 12 July 2021. https://datatracker.ietf.org/doc/html/draft-ounsworth-pq-composite-sigs-05 |
| [PQECK] | Explicit Pairwise Composite Keys For Use In Internet PKI, M. Ounsworth and S. Mister, Internet-Draft, 12 July 2021. https://datatracker.ietf.org/doc/html/draft-ounsworth-pq-explicit-composite-keys-00 |
| [PQTLS12] | Hybrid Post-Quantum Key Encapsulation Methods (PQ KEM) for Transport Layer Security 1.2 (TLS), M. Campagna and E. Crockett, Internet-Draft, 2 September 2021. https://datatracker.ietf.org/doc/html/draft-campagna-tls-bike-sike-hybrid |
| [PQTLS13] | Hybrid key exchange in TLS 1.3, D. Stebila, S. Fluhrer and S. Gueron, Internet-Draft, 13 July 2021. https://datatracker.ietf.org/doc/html/draft-ietf-tls-hybrid-design |
| [PQSSH] | Post-quantum public key algorithms for the Secure Shell (SSH) protocol, P. Kampanakis, D. Stebila, M. Friedl, T. Hansen and D. Sikeridis, Internet-Draft, 21 October 2020. https://datatracker.ietf.org/doc/html/draft-kampanakis-curdle-pq-ssh-00 |
| [PQM4] | Post-quantum crypto library for the ARM Cortex-M4, https://github.com/mupq/pqm4. |
| [PST] | Benchmarking Post-Quantum Cryptography in TLS, C. Paquin, D. Stebila and G. Tamvada, PQCrypto 2020. https://eprint.iacr.org/2019/1447 |
| [QSPKE] | Quantum-Safe Public-Key Encryption and Key Encapsulation, ETSI, TR 103 823 V1.1.1, Septembe 2021. https://www.etsi.org/deliver/etsi_tr/103800_103899/103823/01.01.01_60/tr_103823v010101p.pdf |
| [QSS] | Quantum-Safe Signatures, ETSI, TR 103 616 V1.1.1, September 2021. https://www.etsi.org/deliver/etsi_tr/103600_103699/103616/01.01.01_60/tr_103616v010101p.pdf |
| [Ros] | (1, 2) PQC Transition - ANSSI Views, Mélissa Rossi, PQCrypto 2021. http://pqcrypto2021.kr/download/program/PQC_transition_in_France.pdf |
| [RFC8017] | PKCS #1: RSA Cryptography Specifications Version 2.2, K. Moriarty, B. Kaliski, J. Jonsson and A. Rusch, IETF, RFC 8017, November 2016. https://www.rfc-editor.org/rfc/rfc8017.html |
| [RFC8391] | XMSS: eXtended Merkle Signature Scheme, A. Huelsing, D. Butin, S. Gazdag, J. Rijneveld, and A. Mohaisen, IRTF, RFC 8391, May 2018. https://www.rfc-editor.org/rfc/rfc8391.html |
| [RFC8554] | Leighton-Micali Hash-Based Signatures, D. McGrew, M. Curcio and S. Fluhrer, IRFT, RFC 8554, April 2019. https://www.rfc-editor.org/rfc/rfc8554.html |
| [SBKAM] | The First Collision for Full SHA-1, M. Stevens, E. Bursztein, P. Karpman, A. Albertini and Y. Markov, CRYPTO 2017. https://doi.org/10.1007/978-3-319-63688-7_19 |
| [Shor] | Algorithms for quantum computation: discrete logarithms and factoring, P. W. Shor, 35th Annual Symposium on Foundations of Computer Science, 1994. https://doi.org/10.1109/SFCS.1994.365700 |
| [SP80056A] | Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography, E. Barker, L. Chen, A. Roginsky, A. Vassilev and R. Davis, NIST Special Publication 800-56A Revision 3, April 2018. https://doi.org/10.6028/NIST.SP.800-56Ar3 |
| [SP80056B] | Recommendation for Pair-Wise Key Establishment Using Integer Factorization Cryptography, E. Barker, L. Chen, A. Roginsky, A. Vassilev, R. Davis and S. Simon, NIST Special Publication 800-56B Revision 2, March 2019. https://doi.org/10.6028/NIST.SP.800-56Br2 |
| [SP80056C] | Recommendation for Key-Derivation Methods in Key-Establishment Schemes, E. Barker, L. Chen and R. Davis, NIST Special Publication 800-56C Revision 2, August 2020. https://doi.org/10.6028/NIST.SP.800-56Cr2 |
| [SP800131A] | Transitioning the Use of Cryptographic Algorithms and Key Lengths, E. Barker and A. Roginsky, NIST Special Publication 800-131A Revision 2, March 2019. https://doi.org/10.6028/NIST.SP.800-131Ar2 |
| [SP800208] | (1, 2) Recommendation for Stateful Hash-Based Signature Schemes, D. A. Cooper, D. C. Apon, Q. H. Dang, M. S. Davidson, M. J. Dworkin and C. A. Miller, NIST Special Publication 800-208, October 2020. https://doi.org/10.6028/NIST.SP.800-208 |
| [TW] | One Bit is All It Takes: A Devastating Timing Attack on BLISS’s Non-Constant Time Sign Flips, M. Tibouchi and A. Wallet, Mathcrypt 2019. https://eprint.iacr.org/2019/898 |
| [WYY] | Finding Collisions in the Full SHA-1, X. Wang, Y. Lisa Yin and H. Yu, CRYPTO 2005. https://doi.org/10.1007/11535218_2 |