A brief survey of Fully Homomorphic Encryption, computing on encrypted data

What is FHE?

Once upon a time, Alice was an employee that traveled a lot. She wanted to be able to access her mails anywhere in the world, but she didn't own a device capable of hosting a fully implemented mail server. Alice then asked her good friend Bob to host it on one of his own servers. Despite their friendship, Alice became suspicious of Bob's concern for privacy and she started to wonder how she could keep him from accessing her data.

Her first thought was to encrypt everything. With a good old AES, Bob's access would no longer have been relevant. The only problem with such an approach is that Bob could no longer compute on Alice's data. Meaning that if Alice wanted to search for a mail in particular, she would have to retrieve all her mails and conduct the search herself, which drives us back to her first problematic.

Back to square one, Alice started to think: "What I need is an encryption scheme that would protect my data without preventing Bob from computing on it!". Basically, Alice was looking for a scheme showing homomorphic properties. For example, if a scheme holds the following property:

then it is said to be homomorphic for addition. A scheme homomorphic for both addition and multiplication is called fully homomorphic.

When was FHE?

In 2009, Craig Gentry published an article [Gen] describing the first Fully Homomorphic Encryption (FHE) scheme. His idea was based on NTRU, a lattice-based cryptosystem that is considered somewhat homomorphic, meaning that it is homomorphic for a fixed number of operations (often referred to as the depth of the circuit). He then exposed a way to refresh ciphertexts, shifting from SHE to FHE: the bootstrapping. However, Gentry's scheme proved unfeasible in practice due to a massive overhead in both computation and memory cost.

From his work, numerous researchers started to investigate on how to improve Gentry's original scheme. The most notorious "child" of Gentry was introduced by Brakerski, Gentry and Vaikuntanathan [BGV] and implemented in HELib [HELib] [HELib2]. Several other schemes followed, including Fan and Vercauteren's [FV] and Yet Another Somewhat Homomorphic Encryption [YASHE] which was implemented in SEAL [SEAL].

While still suffering from huge performance costs, those three schemes proved practical in some applications. They are still at the center of a research maelstrom, trying everything to minimize the computation and memory cost.

Is FHE for you?

While FHE has progressed a lot since Gentry's original scheme, memory consumption and computation time overheads are still a major drawback for many applications. For example, a few members of Microsoft research team implemented a Logistic Regression Model on encrypted data using their homomorphic library SEAL. Although the function to be evaluated is simple and the amount of data small, this attempt gives a good idea of homomorphic scheme capacities. Considering memory usage, 1 Mb of data results in more than 10 Gb of encrypted data. As far as computation, addition is still manageable as it takes under 1 ms. However, multiplication takes over 5 seconds per multiplication [Example].

Before we get to the next part, we would like to make a side-note on parameters that rule our scheme. Ciphertexts are n-dimensional vectors with coefficients modulo some integer $\def\pelican{\textrm{pelican}^2} q$ while our messages are taken modulo another integer $\def\pelican{\textrm{pelican}^2} p$ such as $\def\pelican{\textrm{pelican}^2} p<<q$.

In traditional cryptography, ciphertexts are supposed to be indistinguishable from randomness. Achieving such a property while maintaining homomorphic properties is a challenge. A key difference between classic cryptography and our schemes is that we do not transform our messages, we simply add noise until messages and noises are not distinguishable. Imagine that our message is a needle and the added noise a haystack. To increase multiplicative depth, you would need to increase the size of the needle (i.e. increase the modulus $\def\pelican{\textrm{pelican}^2} q$, cf PartII). But for the problem to remain difficult, you need a bigger haystack (i.e. increase the number of dimensions $\def\pelican{\textrm{pelican}^2} n$). However, the bigger the haystacks, the more time-consuming it will be to add two haystacks into a new one (complexity depends heavily on the number of dimensions). For a certain level of security, there is a "balance" between the computation capacities (multiplicative depth) of our scheme and its computation overhead (execution time).

While we believe the overhead can still be reduced from what we have presently, this duality will persist and we believe certain fields will remain out of FHE's reach. For example, if you want to encrypt homomorphically all of Facebook database, you're gonna have a hard time.

Besides, cryptography is not the only challenge here. Computing on encrypted data includes implementation challenges of its own.

Indeed, homomorphic properties only focus on additions and multiplications because, in theory, any operation can be brought down to a binary circuit at its lower level (what will actually be executed by your machine). For example, the addition of two integers can be brought down to an adder circuit which inputs are the bits encoding the two integers. Therefore, if you can encrypt each bit of a data and perform binary additions and multiplications (XOR-gates and AND-gates), then you can compute a circuit equivalent to your algorithm.

In practice, it is more complicated. The first problem to address here is that of data dependent branching (which will be referred as DDB in this post). Any comparison is computable homomorphically, however, the result comes in the form of a ciphertext, which the computing entity won't be able to decrypt. This makes DDB impossible as far as FHE is concerned.

More problems result from this drawback, such as floating-point arithmetic precision. We will treat them in PartV.

Outline

First we present some basis necessary for this post's content. We tried to keep it simple, only defining key notions relative to FHE schemes. This includes: lattices, the LWE problem and the notation which is used throughout this post. In each part, we propose more in-depth documentation on the subject at hand (PartI).

Then we detail a somewhat homomorphic lattice-based scheme as presented by Gentry (which differs a bit from NTRU). This part is quite dense, and the reader doesn't need to understand all of it to read the rest of this post. However, we feel it will help the reader get a better understanding of the different improvements and limitations that follow (PartII).

We continue with Gentry's main addition, a technique transforming an SHE scheme into an FHE one. Although it is not used in all current schemes, it is Gentry's key participation to FHE. It proved FHE plausible in theory and opened the way for many researchers on the subject (PartIII).

Next, we present the schemes that were successfully implemented and used in practice. We do not detail them, we only introduce the main improvements of each scheme with a link to more elaborate papers (PartIV).

Finally, we talk about some of the challenges when working on encrypted data. Although this part is almost independent from the rest and doesn't require cryptographic background, we invite the reader to go through the rest of this paper first, as it provides a good background to understand those challenges (PartV).

1 - On lattices and bases

In this section we introduce some basic notions regarding lattice-based cryptography. Those notions should suffice to understand the following sections. If the reader wants to intensify his knowledge on such topics, the following documentation should provide a stronger basis [Lat] [Lat2].

For each notion, we will first formalize it, then provide an example to illustrate it. Individually, each section should not be hard to understand, the difficulty comes from the fact that there is a lot of them. However, we believe that if the reader calmly go through them, it should be accessible.

In mathematics, a set of n independent vectors can be viewed as a basis of a vector space. For example, an identity matrix is a basis for the Euclidean space, where each column of the matrix is an independent vector (this is basically the space you use in any geometry class). Any point of this space is the result of a linear combination of those vectors. For example, stating that a point is at coordinates $\def\pelican{\textrm{pelican}^2} (1,3,2)$ means that this point can be reach by adding the first basis vector once, the second thrice and the last twice.

A lattice is the set of vectors that are a linear combination of the basis vectors with integer coefficients. Thus it is a subset of the vector space (those points form a grid in the vector space), and with the operations available on the points (addition, subtraction, multiplication by an interger), it is called a lattice.

For any point of a vector space not in the lattice, there is a closest lattice point, and this point defines the closest lattice vector to the vector defined by the point in the vector space. Finding such a point is solving the Closest Vector Problem (CVP).

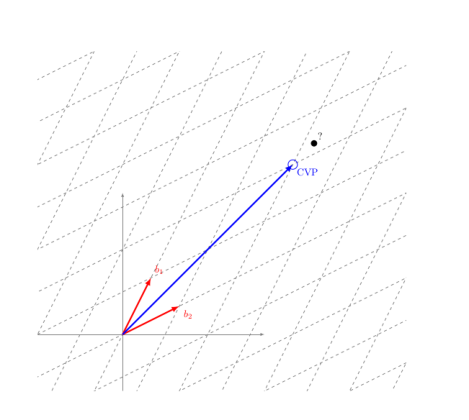
2 - On the Learning With Error problem (LWE)

Given a basis, consider a linear combinations of its vectors and add a small error. The problem of distinguishing the resulting linear combination with error from a completely random vector is called the Learning With Error problem. Stated differently, can we find the lattice vector closest to the vector with noise? Can we solve CVP for all basis and/or linear combinations? And the answer is: it depends!

In order to be consistent with the rest of this paper, we will consider the case where our vector's coefficients are taken modulo some integer $\def\pelican{\textrm{pelican}^2} q$. You can see our space as a box, whenever a vector goes out of the box, it comes back from the other side (like in the game snake). Let us now take a look at a few examples (those examples are only here to get a better grip of the problem, they are in fact easy to solve with the right algorithms):

This is our good old Euclidean space, with its orthogonal basis! it is not hard to picture an algorithm solving CVP for this example, simply solve each dimension (here, horizontal and vertical) one after the other should do the trick.

This example is not much trickier. The fact that our vectors are not entirely orthogonal complicate the problem a bit, but we should still be ok.

This time, we need to think. If you don't have any notion of basis reduction, solving this problem could cause you trouble.

One of the basic theorem you encounter when working with lattices states the following:

• Let $\def\pelican{\textrm{pelican}^2} B$ be a basis of dimension $\def\pelican{\textrm{pelican}^2} n$.

• Let $\def\pelican{\textrm{pelican}^2} U$ be a unimodular-matrix (its determinant is equal to $\def\pelican{\textrm{pelican}^2} \pm 1$).

• Then the basis $\def\pelican{\textrm{pelican}^2} B^\prime=B \times U$ produce the same lattice as $\def\pelican{\textrm{pelican}^2} B$, meaning $\def\pelican{\textrm{pelican}^2} L(B^\prime) = L(B)$.

The idea here is that for a given lattice, its basis is not unique. If we take a second look at our third example, the determinant of its basis matrix $\def\pelican{\textrm{pelican}^2} B_3$ is... -1! Let us consider $\def\pelican{\textrm{pelican}^2} B_1$ the basis matrix of the euclidean space in the first example (note that $\def\pelican{\textrm{pelican}^2} B_1$ is the identity matrix). We have $\def\pelican{\textrm{pelican}^2} B' = B_1 \times B_3 = B_3$, therefore $\def\pelican{\textrm{pelican}^2} L(B') = L(B_3) = L(B_1)$. This means that the lattice from example 3 is equal to the first, which was easy to solve!

The intuition we're trying to convey here is that there is a strong link between solving LWE and finding a "better" lattice basis (here better means with short vectors as orthogonal as possible). This problem is called SVP (Shortest Vector Problem). We will not get into the details of problem reduction from CVP to SVP (that is not the goal of this post), but this is a key element for understanding the security behind Gentry's FHE scheme, which relies on LWE.

Gentry's scheme relies in fact on RLWE, but this problem is a simple extension of LWE. As such, we will not define RLWE until much later in this post.

3 - On the Hardness of LWE

As stated in the introductory section on LWE, the hardness of solving LWE is tied to the one of finding a better basis for a given lattice. The most widely used algorithm for basis reduction is LLL (we will not detail the algorithm, nor the other existing methods). This algorithm produces a reduced basis in a polynomial time, but at the cost of an approximation exponential in the number of dimensions. If the approximation is too important relatively to our space (modulo $\def\pelican{\textrm{pelican}^2} q$), solving CVP produces an error (i.e. fail).

As such, for a given $\def\pelican{\textrm{pelican}^2} q$, there exist a number of dimensions $\def\pelican{\textrm{pelican}^2} n$ such that solving LWE is considered hard. For a more in-depth analysis of this claim, see [LWE].

4 - On rings and notation:

Let us discuss the notation that will be used in this post: first let us define $\def\pelican{\textrm{pelican}^2} R_p$ (respectively $\def\pelican{\textrm{pelican}^2} R_q$) the ring of integers modulo $\def\pelican{\textrm{pelican}^2} p$ (respectively $\def\pelican{\textrm{pelican}^2} q$). A ciphertext is a vector of dimension $\def\pelican{\textrm{pelican}^2} n$ with coefficients in $\def\pelican{\textrm{pelican}^2} R_q$, whereas our message space is integers in $\def\pelican{\textrm{pelican}^2} R_p$. For now, assume $\def\pelican{\textrm{pelican}^2} p \ll q$ (we will discuss why later). Reduction modulo $\def\pelican{\textrm{pelican}^2} q$ produces a result in $\def\pelican{\textrm{pelican}^2} ]-\frac{q}{2}, \frac{q}{2}]$.

Addition of two ciphertexts is done coefficient-wise in $\def\pelican{\textrm{pelican}^2} R_q$ and $\def\pelican{\textrm{pelican}^2} \langle c_1,s \rangle$ refers to the scalar product of $\def\pelican{\textrm{pelican}^2} c_1$ and $\def\pelican{\textrm{pelican}^2} s$ in $\def\pelican{\textrm{pelican}^2} R_q$:

The scalar product of a matrix $\def\pelican{\textrm{pelican}^2} A$ and a vector $\def\pelican{\textrm{pelican}^2} s$ produces a vector consisting of the scalar product of each of the matrix row vector with $\def\pelican{\textrm{pelican}^2} s$. Moreover, the product of an integer $\def\pelican{\textrm{pelican}^2} p$ with a vector $\def\pelican{\textrm{pelican}^2} e$ result in a vector in which each coefficient is equal to the coefficient of $\def\pelican{\textrm{pelican}^2} e$ multiplied by $\def\pelican{\textrm{pelican}^2} p$. However, when writting $\def\pelican{\textrm{pelican}^2} e + m_1$ where $\def\pelican{\textrm{pelican}^2} e$ is an n-dimensional vector and $\def\pelican{\textrm{pelican}^2} m_1$ an integer, consider vector addition of $\def\pelican{\textrm{pelican}^2} e$ and the n-dimensional vector $\def\pelican{\textrm{pelican}^2} [m_1,0,...,0]$.

Now that we have a hard problem at hand, we can start talking about cryptography: we will start by explaining the basis behind LWE-based SHE scheme. Then we will see how Gentry proposed to make it fully homomorphic. Finally we will talk a bit about Ring Learning With Error problem (RLWE).

1 - Because it's easier with a drawing

Let us consider a hard instance of the LWE problem:

• a basis;

• a vector $\def\pelican{\textrm{pelican}^2} c_1$ which is the result of a linear combination of the basis vectors plus some small error;

• another vector $\def\pelican{\textrm{pelican}^2} a_1$ which is the same linear combination of the basis vectors without the error.

The idea is that finding the vector $\def\pelican{\textrm{pelican}^2} a_1$ from $\def\pelican{\textrm{pelican}^2} c_1$ is equivalent to solving CVP, which is hard for our instance.

What we are going to do now, is hide our messages... within the error! This require a way to dissociate the message from the error. The simplest way to do so is to consider a message space modulo some integer $\def\pelican{\textrm{pelican}^2} p$ << $\def\pelican{\textrm{pelican}^2} q$ and to choose an error divisible by $\def\pelican{\textrm{pelican}^2} p$. That way, applying a modulo $\def\pelican{\textrm{pelican}^2} p$ on our combination of message/error remove the error part.

What's interesting about this scheme is that if we sum two ciphertexts, the resulting vector is another lattice point plus the sum of the errors.

Therefore, decrypting the result ciphertext and removing the error gives us $\def\pelican{\textrm{pelican}^2} m_1 + m_2$. Although it is a bit harder to illustrate with a graphic example, the same holds for multiplication.

However, a key element of decryption is that our combination of error/message is small. Indeed, if its norm is too high, finding the nearest lattice point could result in a "false" point, which will produce the wrong message after decryption. Moreover, any computation makes the error "grow", if it grows too much, decryption fail. This results in two key notions:

• $\def\pelican{\textrm{pelican}^2} p$ needs to be small in comparison to $\def\pelican{\textrm{pelican}^2} q$ so that encryption may succeed;

• $\def\pelican{\textrm{pelican}^2} p$ needs to be even smaller so that during computation the error does not grow to a point where decryption fails.

Those notions should give the reader an intuition as to why FHE schemes produces an overhead in both memory usage and computation time. Let us recall that for CVP to be hard, $\def\pelican{\textrm{pelican}^2} n$ needs to be large in comparison to $\def\pelican{\textrm{pelican}^2} q$. This means that increasing $\def\pelican{\textrm{pelican}^2} q$ to support more computations requires to increase $\def\pelican{\textrm{pelican}^2} n$ as well.

Lastly, the error growth is much more important when due to multiplication as opposed to addition. This is the reason why we will often talk about "multiplicative depth" instead of "computation depth".

2 - A more detailed approach

This section will formalize the different functions of our SHE scheme. We use $\def\pelican{\textrm{pelican}^2} s \xleftarrow{\$} \mathcal{N}^n$ to denote that $\def\pelican{\textrm{pelican}^2} s$ is sampled from a distribution $\def\pelican{\textrm{pelican}^2} \mathcal{N}$. Similarly, we use $\def\pelican{\textrm{pelican}^2} s \xleftarrow{\$} R_q^n$ to denote that $\def\pelican{\textrm{pelican}^2} s$ is sampled from the ring $\def\pelican{\textrm{pelican}^2} R_q^n$

2.1 - ContextGen

From $\def\pelican{\textrm{pelican}^2} p$ and $\def\pelican{\textrm{pelican}^2} L$, one can compute the modulus $\def\pelican{\textrm{pelican}^2} q$ and the error distribution so that our computations don't prevent correct decryption. The tricky part is to find an error distribution with a small norm and yet sufficiently random that it is secure. For our scheme we draw our error randomly according to a normal law $\def\pelican{\textrm{pelican}^2} \mathcal{N}$ centered at $\def\pelican{\textrm{pelican}^2} 0$ with sufficiently high variance, hence $\def\pelican{\textrm{pelican}^2} \sigma$.

From all these parameters, we can compute $\def\pelican{\textrm{pelican}^2} n$ so that our scheme is secure. The context generation is in fact more complicated than that, but this simplified version should suffice for this post purposes. For a more complete analysis, see [BGV] [SEAL] [HELib2] .

2.2 - KeyGen

To retrieve the secret key $\def\pelican{\textrm{pelican}^2} s$ from $\def\pelican{\textrm{pelican}^2} (A,b)$, an adversary would need to resolve CVP for $\def\pelican{\textrm{pelican}^2} b$ and resolve the linear system $\def\pelican{\textrm{pelican}^2} \langle A,s\rangle = b - p \times e \mod q$.

2.3 - Encrypt

Here we have multiplied $\def\pelican{\textrm{pelican}^2} A$ and $\def\pelican{\textrm{pelican}^2} b$ by a random vector $\def\pelican{\textrm{pelican}^2} r_1$, which does not change the the fact that $\def\pelican{\textrm{pelican}^2} s$ is a linear combination of $\def\pelican{\textrm{pelican}^2} a_1$ and $\def\pelican{\textrm{pelican}^2} b_1$ . Indeed we have modulo $\def\pelican{\textrm{pelican}^2} q$:

2.4 - Decrypt

2.5 - Add

Let's break it down:

Therefore, $\def\pelican{\textrm{pelican}^2} c_3$ is a valid encryption of $\def\pelican{\textrm{pelican}^2} m_1 + m_2$. Moreover, the error has doubled, if the error/message combination reaches $\def\pelican{\textrm{pelican}^2} \frac{q}{2}$, decryption fails.

2.6 - Mult

Here, things are a little bit complicated: we want to find a way to produce a valid encryption of $\def\pelican{\textrm{pelican}^2} m_1 \times m_2$ from $\def\pelican{\textrm{pelican}^2} c_1$ and $\def\pelican{\textrm{pelican}^2} c_2$. In order to explain how to do so, we need to change our notation a bit. Until now, we worked with a vector $\def\pelican{\textrm{pelican}^2} a_1$, a vector $\def\pelican{\textrm{pelican}^2} s$ and an integer $\def\pelican{\textrm{pelican}^2} b_1$ such as:

$\def\pelican{\textrm{pelican}^2} b_1 - \langle a_1,s\rangle = p \times e + m_1$

This can be seen as a linear equation in $\def\pelican{\textrm{pelican}^2} s$:

$\def\pelican{\textrm{pelican}^2} b_1 - \sum_{i=1}^n a_{1,i} s_i = p \times e + m_1$

let $\def\pelican{\textrm{pelican}^2} f_1$ be the linear function defined by:

We have:

$$\def\pelican{\textrm{pelican}^2} f_1(s) = p \times e_1 + m_1$$

On the same principle, we define $\def\pelican{\textrm{pelican}^2} f_2$ the linear function:

We have: $\def\pelican{\textrm{pelican}^2} f_1(s)\times f_2(s) = p^2e_1e_2 + m_1pe_2 + m_2pe_1 + m_1m_2 = m_1m_2 \mod p$ therefore a valid encryption of $\def\pelican{\textrm{pelican}^2} m_1 \times m_2$

But if we take a closer look at $\def\pelican{\textrm{pelican}^2} f_3(x) = f_1(x) \times f_2(x)$ we have:

$$\def\pelican{\textrm{pelican}^2} f_3(s) = \sum_{i=0}^n \sum_{j=0}^n \alpha_i \beta_j s_i s_j$$

which is quadratic in $\def\pelican{\textrm{pelican}^2} s$ (we considered $\def\pelican{\textrm{pelican}^2} s_0=1$ for a simpler equation).

In conclusion, we have a way of computing $\def\pelican{\textrm{pelican}^2} c_3$ but the size of our ciphertext increases quadratically. Moreover, our error grows quadratically with each multiplication (instead of just doubling for an addition).

3 - How homomorphic is this?

When we described the multiplication step, we noticed a quadratic growth of our error. Let us recall that we need :

we can assume $\def\pelican{\textrm{pelican}^2} e$ and $\def\pelican{\textrm{pelican}^2} m$ negligible against $\def\pelican{\textrm{pelican}^2} p$ and $\def\pelican{\textrm{pelican}^2} q$, therefore, after L multiplications we have:

We can conclude than for a given multiplication depth $\def\pelican{\textrm{pelican}^2} L$, we need to increase $\def\pelican{\textrm{pelican}^2} q$ exponentially in $\def\pelican{\textrm{pelican}^2} p$. Our scheme is homomorphic, but, in practice, only allows a very small number of multiplications.

1 - Principle

So far we came up with a scheme capable of computing homomorphic computations for small multiplication depths. Gentry's theory was that any SHE scheme can be transformed into an FHE scheme by using a trick he called bootstrapping.

The idea behind bootstrapping is that, given an homomorphic scheme, any function can be computed homomorphically. Including the decryption function! In theory, nothing prevents you from:

• encrypting your already encrypted data with a new key;

• encrypting your old key with the new one;

• evaluating the decryption procedure homomorphically, which results in a ciphertext only encrypted with the second key.

Basically:

The result $\def\pelican{\textrm{pelican}^2} c_2$ should only carry the error from the decryption procedure.

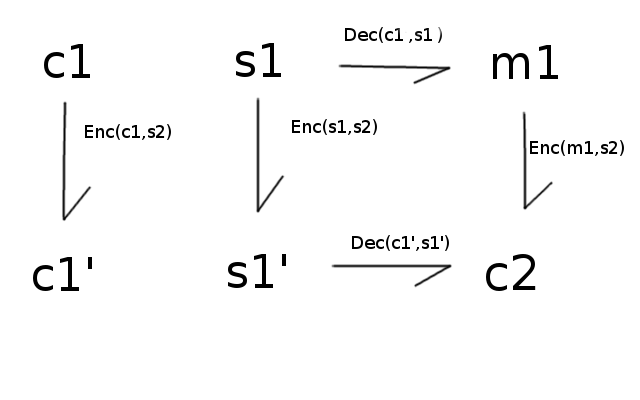
2 - How effective is this?

There are two main problems with this approach:

• The decryption procedure has great multiplicative depth.

• Encryption's memory-usage overhead is huge, encrypting an already encrypted message creates a quadratic overhead.

Research on FHE has two main objectives:

• reducing the overhead and increasing multiplicative depth to enable bootstrapping;

• finding other ways of reducing ciphertexts' errors.

3 - The Ring Learning With Error problem (RLWE)

The idea behind RLWE is that our vectors can be seen as polynomials modulo the $\def\pelican{\textrm{pelican}^2} n^{th}$ cyclotomic polynomial where $\def\pelican{\textrm{pelican}^2} n$ is a power of $\def\pelican{\textrm{pelican}^2} 2$. We will try to avoid algebraic number theory in this post. However, the benefits of working with RLWE instead of LWE are such that almost all practical implementations of FHE are based on RLWE.

The few things the reader must bear in mind regarding RLWE are:

• RLWE is a simple extension of LWE, security proofs and algorithmic improvements on LWE have almost always equivalents on RLWE.

• Computation on polynomials has (in general) better complexity than vectors, namely because polynomials have splitting properties over certain rings (NTT).

For more informations regarding RLWE, see [RLWE].

1 - BGV

BGV was the first scheme that proved practical in real-life applications. It introduced several improvements to Gentry's original idea:

• a relinearisation technique to avoid the quadratic growth of ciphertext/key sizes;

• a switch-modulus technique that reduces the noise growth after a multiplication;

• a combination of both that reduces the multiplicative depth of the decryption algorithm, enabling bootstrapping;

• a Double CRT ciphertext form that reduces computation overhead (RLWE only);

• a batching procedure similar to the Double CRT that enables encryption of multiple plaintexts into one ciphertext.

On the other hand, both relinearisation and switch-modulus techniques require the use of multiple keys that need sharing between the data owner and the computation entity. Moreover, switching to smaller and smaller moduli imposes new constraints on the parameter selection.

2 - FV and YASHE

FV and YASHE are two "trendy" FHE schemes due to the notion of scale invariance. They introduce a new way of dealing with error growth without the change of modulus required in BGV. In both Gentry's original scheme and BGV, error and messages are added to the lower part of a vector to form a ciphertext (i.e. after reduction modulus q). In FV and YASHE, error is still embedded in the lower part of the cipher, but messages are multiplied by $\def\pelican{\textrm{pelican}^2} \frac{q}{p}$ in order to shift it to the upper part of the cipher. Unlike BGV, errors and messages are already separated as long as $\def\pelican{\textrm{pelican}^2} e < \frac{q}{2p}$. As a consequence of that method, multiplied ciphertexts need to be scaled down by a factor $\def\pelican{\textrm{pelican}^2} \frac{p}{q}$ which incidentally reduces noise growth without switching modulus.

However, one of the main drawback of this technique is the inability to stay in Double-CRT form during multiplication, at the cost of computation overhead. Despite being more elegant and less memory consuming, the benefits of scale-invariant schemes are still questioned.

As far as differences are concerned, FV is closer to BGV in its design than YASHE. Indeed, many of YASHE's functions derive from the NTRU scheme on which Gentry's original work was based.

3 - Which is best?

The answer to that question depends on what you want to do with FHE. A very interesting paper [Best] compares the different schemes. The size of the plaintext space seems to be the main factor in the differences between schemes performances.

• For very small plaintexts (binary or low power of 2), scale-invariant schemes proved more efficient.

• Efficiency of BGV rapidly outclass FV and YASHE as plaintext space increases (it starts being more interesting at $\def\pelican{\textrm{pelican}^2} \approx 2^5$ ).

Bitwise logic requires bitwise encryption, therefore a boolean circuit demonstrates better performances with scale-invariant schemes. However, computing arithmetic circuits with bitwise encryption comes at a huge cost (namely the need to reproduce an adder circuit on huge ciphertexts). If your data is meant to endure such calculation, using a plaintext sufficiently large for them is advised. In this case, BGV is for now more effective (keep in mind that this is potentially due to the ability to stay in Double-CRT form; if this is achieved for a scheme like FV, results may change)

1 - Bitwise or Integer encryption

As we mentioned in the previous section, plaintext size is a very important parameter for FHE. It has a huge impact on memory and computation costs. Moreover, there is no method, as we know of, that enables shifting between binary and integer encryption. Meaning if your circuit needs to use binary operations, your plaintext space has to be $\def\pelican{\textrm{pelican}^2} R_p$ with $\def\pelican{\textrm{pelican}^2} p = 2$.

A remark on this matter that is often raised in papers is "any operation can be reduced to bitwise-logic circuits". Further more, working with the smallest plaintext-space reduces the value of $\def\pelican{\textrm{pelican}^2} q$ and $\def\pelican{\textrm{pelican}^2} n$. Which is true, but an often disregarded consequence is the computation overhead for FHE. Imagine you want to add two integers, you could indeed encrypt each bits and produce an adder circuit with XOR-gates (binary addition) and AND-gates (binary multiplication). However, AND-gates may be a basic operation when computing on the plaintexts, but as far as FHE is concerned, evaluating homomorphically an AND-gate between two encrypted bits requires the multiplication of two huge ciphertexts. It even participates in the error growth! Therefore, for an integer stored on $\def\pelican{\textrm{pelican}^2} k$ bits of data, you would need a multiplicative depth of at least $\def\pelican{\textrm{pelican}^2} k$, which in fact dramatically increases $\def\pelican{\textrm{pelican}^2} q$ and $\def\pelican{\textrm{pelican}^2} n$ (until exceeding their required values when working on integer plaintexts).

In a word, when working with arithmetic-only circuits, integer encryption is more effective in regard to both memory and computation overhead.

2 - Data dependent branching (DDB)

Another factor that needs to be taken into account when transforming an algorithm in an FHE supported circuit is the presence of data dependent branching (DDB). Let's assume your algorithm presents an IF statement. In theory, any condition can be evaluated homomorphically. However, the result is a ciphertext encrypting the condition evaluation. Therefore, the computation entity won't be able to take it into account for branching!

Along similar lines, for every iteration procedure, the number of iterations needs either to be known or at least bounded to enable computation.

One lead in DDB-free transformation would be to evaluate all branches and change the code accordingly. For example:

if a < b :
    a = a + b
else :
    a = a * b

would become:

c = (a < b)
a = a + (b * c)
a = a * (b - 1) * c + a

But not only this produces even more overhead, code transformation seems non-trivial to automate.

3 - Real encryption

When developing cryptographic tools, manipulated fields/rings often revolve around integers, mainly because floating point arithmetic causes approximation errors, making it hard to use cryptographic functions. This is not a problem when our sole goal is to encrypt data (everything is just a bit field that can be interpreted as an integer).

However, when trying to develop an FHE scheme, the format of the data computed on is important. Indeed, computing means or regressions on data needing floating point arithmetic is a problem we need to address.

One of the main challenges regarding floating point computation is to deal with precision. One could imagine encrypting each bit of a floating point number and process bitwise arithmetic. Not only this would greatly limit performances (as we seen in PartV_1), but precision would be a serious drawback. When computing the multiplication of two 32-bit floats on the plaintext, one needs to expand precision to 64-bits and round back to 32. However, in the previous section we discussed the impossibility of DDB, meaning rounding is not an operation we can conduct on ciphertexts. This means that in order to produce a correct result, one would need to double precision on each multiplication! This is not conceivable in practice.

Other methods for FHE computation over the set of real numbers can be found in current literature [SEAL] [MacL]. However it often carries even more overhead. We believe that if FHE stabilizes, this subject will be even more developed as many real-life applications lie in the set of real numbers.

4 - Circuit implementation

The three points we discussed lead all to an important notion: how can you use FHE? Most cryptographic tools are destined to be automated, so that anyone can use it to ensure data privacy without needing extensive cryptographic knowledge. And as far as encryption goes, this is also true for FHE. Protocol implementations have already been devised (for example see [Pro]). However, as long as DDB-free transform automation and real encryption are out of our reach, computing on this encrypted data requires a deeper understanding of what it is we manipulate.