Differential Fault Analysis on White-box AES Implementations

With the Differential Computation Analysis (DCA) presented at CHES 2016, we have shown that side-channel techniques developed to break hardware cryptographic implementations can be adapted successfully to break white-box implementations. In this post, we will explore another class of hardware attacks: fault injections and how to apply them on white-box implementations.

Disclaimer: it is possible to mount fault attacks on DES but in this post we will focus only on AES.

Introduction

Applying fault attacks against white-box implementations is not new. Indeed, shortly after the pre-publication of our DCA attacks against a few white-box challenges [1], Sanfelix, Mune and de Haas presented successful Differential Fault Analysis (DFA) attacks against the same white-box challenges at BlackHat Europe 2015 [2].

We must recognize that when we started investigating side-channel techniques, we did not dare to look at fault injections against white-boxes because it seemed over-complicated. Indeed, many recent DFA papers focus on reducing the number of required faults at the price of an increased complexity to brute-force parts of the key, and sometimes they require fine control on the location or the type of injected faults.

Faulting a recent smartcard is difficult, with a high risk to cause the chip to self-destruct if it detects an attack; that is why recent DFA research try to minimize the requirements on the number of faults. But in the white-box attack model, faults are very easy and cheap to perform and do not lead to the program self-destruction as of now :). Therefore applying the first DFA attack described in 2002 [3] is probably one of the best strategies in the white-box context:

It is easy to understand, which is a quite compelling property given that we have to implement it by ourselves and guess some missing parts in its description.
It is using a very practical fault model with nice properties that allow to shoot randomly at the white-box implementation and sort out the exploitable results.

AES encryption

But first, let us recap how AES works in simple words (if you want a formal definition, the best is to read more reliable sources than this post, e.g. Wikipedia;) ).

It is composed of 10, 12 or 14 rounds (for respectively AES-128, AES-192 and AES-256) transforming progressively the 16-byte input (referred to as "state" and conveniently represented as a $\def\pelican{\textrm{pelican}^2} 4 \times 4$ square matrix with values in $\def\pelican{\textrm{pelican}^2} GF(2^8)$ ) through repeated operations that we will detail briefly, and mixing it progressively with 16-byte so-called round keys. An initial round key is used at the very beginning so in total you get respectively 11, 13 or 15 round keys that we will label as $\def\pelican{\textrm{pelican}^2} K_{0} \ldots K_{10}, K_{12}, K_{14}$ .

Round keys are derived from the AES key through a key scheduling that expands the AES key to cover all the round keys. This means that in AES-128, the first round key is the AES key, while in AES-256 the key is split into the first two round keys (and an AES-192 key covers the first one and a half round keys). Of course, in the white-box context, the key scheduling is never performed in situ but pre-computed when the white-box is generated (and the AddRoundKey is blended in the other round operations in an attempt to hide the round keys).

The operations performed in each round are, for an encryption, the following ones:

SubBytes, the only non-linear operation. It is a substitution based on a S-Box mapping each byte value to another one.
ShiftRows, shifting the rows of the $\def\pelican{\textrm{pelican}^2} 4 \times 4$ state matrix.
MixColumns, a linear transformation of each column. You can see it as a $\def\pelican{\textrm{pelican}^2} 4 \times 4$ matrix multiplication applied on the state. It is the only operation mixing different bytes of the state together.
AddRoundKey, a simple XOR between the state and a round key.

The last round is shorter as it does not perform the MixColumns operation.

DFA on AES-128 Encryption

Let us present briefly the DFA attack described by Dusart, Letourneux and Vivolo in 2002 [3].

The general requirements of a DFA attack are:

The output must be observable without external encoding (directly at the end of the cipher or somewhere else in the application once it gets decoded).
It must be possible to execute the cipher several times on the same input (which can be encoded or unknown). Capturing the state of the AES after a few rounds and restoring it multiple times is also an option.

The basis of the attack is that one byte of the state needs to be corrupted somewhere between the two last MixColumns operations, which take place in the last 3 rounds. Below is a reminder of the operations of the last 3 rounds for AES-128:

SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{8}$
SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{9}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{10}$

If one byte is modified between those two MixColumns, only one single MixColumns has still to be computed on the faulty state and the fault will be propagated to exactly 4 bytes of the output.

How?

Let us write the AES state as follows and let us compare it with a version where we fault the first byte just before the last MixColumns operation:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} A & E & I & M \\ B & F & J & N \\ C & G & K & O \\ D & H & L & P \end{pmatrix} \text{and} \begin{pmatrix} X & E & I & M \\ B & F & J & N \\ C & G & K & O \\ D & H & L & P \end{pmatrix}

The fault could occur earlier (but after the penultimate MixColumns). However, as we do not make any assumption on the value of the fault and as ShiftRows is only moving the faulty byte around, where the fault happens does not change our reasoning. Thus the remaining operations are:

MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{9}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{10}$

Which gives successively the following states (non affected elements are omitted for clarity).

After MixColumns (here the multiplication is done in the Galois Field, see e.g. Wikipedia's explanations:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} 2A+3B+C+D & \cdots & \cdots & \cdots \\ A+2B+3C+D & \cdots & \cdots & \cdots \\ A+B+2C+3D & \cdots & \cdots & \cdots \\ 3A+B+C+2D & \cdots & \cdots & \cdots \end{pmatrix} \text{and} \begin{pmatrix} 2X+3B+C+D & \cdots & \cdots & \cdots \\ X+2B+3C+D & \cdots & \cdots & \cdots \\ X+B+2C+3D & \cdots & \cdots & \cdots \\ 3X+B+C+2D & \cdots & \cdots & \cdots \end{pmatrix}

After AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{9}$ (the addition in the Galois Field is identical to the binary operator XOR):

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} 2A+3B+C+D+K_{9,0} & \cdots & \cdots & \cdots \\ A+2B+3C+D+K_{9,1} & \cdots & \cdots & \cdots \\ A+B+2C+3D+K_{9,2} & \cdots & \cdots & \cdots \\ 3A+B+C+2D+K_{9,3} & \cdots & \cdots & \cdots \end{pmatrix} \text{and} \begin{pmatrix} 2X+3B+C+D+K_{9,0} & \cdots & \cdots & \cdots \\ X+2B+3C+D+K_{9,1} & \cdots & \cdots & \cdots \\ X+B+2C+3D+K_{9,2} & \cdots & \cdots & \cdots \\ 3X+B+C+2D+K_{9,3} & \cdots & \cdots & \cdots \end{pmatrix}

After SubBytes:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} S(2A+3B+C+D+K_{9,0}) & \cdots & \cdots & \cdots \\ S(A+2B+3C+D+K_{9,1}) & \cdots & \cdots & \cdots \\ S(A+B+2C+3D+K_{9,2}) & \cdots & \cdots & \cdots \\ S(3A+B+C+2D+K_{9,3}) & \cdots & \cdots & \cdots \end{pmatrix} \text{and} \begin{pmatrix} S(2X+3B+C+D+K_{9,0}) & \cdots & \cdots & \cdots \\ S(X+2B+3C+D+K_{9,1}) & \cdots & \cdots & \cdots \\ S(X+B+2C+3D+K_{9,2}) & \cdots & \cdots & \cdots \\ S(3X+B+C+2D+K_{9,3}) & \cdots & \cdots & \cdots \end{pmatrix}

After ShiftRows:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} S(2A+3B+C+D+K_{9,0}) \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S(A+2B+3C+D+K_{9,1})\\ \cdots \qquad \cdots \qquad S(A+B+2C+3D+K_{9,2}) \qquad \cdots \\ \cdots \qquad S(3A+B+C+2D+K_{9,3}) \qquad \cdots \qquad \cdots \end{pmatrix} \text{and} \begin{pmatrix} S(2X+3B+C+D+K_{9,0}) \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S(X+2B+3C+D+K_{9,1})\\ \cdots \qquad \cdots \qquad S(X+B+2C+3D+K_{9,2}) \qquad \cdots \\ \cdots \qquad S(3X+B+C+2D+K_{9,3}) \qquad \cdots \qquad \cdots \end{pmatrix}

And finally after AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{10}$ :

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} S(2A+3B+C+D+K_{9,0})+K_{10,0} \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S(A+2B+3C+D+K_{9,1})+K_{10,13}\\ \cdots \qquad \cdots \qquad S(A+B+2C+3D+K_{9,2})+K_{10,10} \qquad \cdots \\ \cdots \qquad S(3A+B+C+2D+K_{9,3})+K_{10,7} \qquad \cdots \qquad \cdots \end{pmatrix} \text{and} \begin{pmatrix} S(2X+3B+C+D+K_{9,0})+K_{10,0} \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S(X+2B+3C+D+K_{9,1})+K_{10,13}\\ \cdots \qquad \cdots \qquad S(X+B+2C+3D+K_{9,2})+K_{10,10} \qquad \cdots \\ \cdots \qquad S(3X+B+C+2D+K_{9,3})+K_{10,7} \qquad \cdots \qquad \cdots \end{pmatrix}

Looking, for example, at the first byte of the output, we get the following equations for the normal and faulty cases:

\def\pelican{\textrm{pelican}^2} O_0 = S(2A+3B+C+D+K_{9,0})+K_{10,0}

\def\pelican{\textrm{pelican}^2} O'_0 = S(2X+3B+C+D+K_{9,0})+K_{10,0}

XORing them (that is why it is called differential fault analysis):

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S(2A+3B+C+D+K_{9,0})+K_{10,0} + S(2X+3B+C+D+K_{9,0})+K_{10,0}

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S(2A+3B+C+D+K_{9,0}) + S(2X+3B+C+D+K_{9,0})

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S(2A+3B+C+D+K_{9,0}) + S(2X+\mathbf{2A+2A}+3B+C+D+K_{9,0})

If we pose:

\def\pelican{\textrm{pelican}^2} Y_0=2A+3B+C+D+K_{9,0}

\def\pelican{\textrm{pelican}^2} Z=A+X

This becomes:

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S(Y_0) + S(2Z+Y_0)

Similar equations can be written for the three other output bytes affected by the fault:

\def\pelican{\textrm{pelican}^2} O_7 + O'_7 = S(Y_1) + S(3Z+Y_1)

\def\pelican{\textrm{pelican}^2} Y_1 = 3A+B+C+2D+K_{9,3}

\def\pelican{\textrm{pelican}^2} O_{10} + O'_{10} = S(Y_2) + S(Z+Y_2)

\def\pelican{\textrm{pelican}^2} Y_2 = A+B+2C+3D+K_{9,2}

\def\pelican{\textrm{pelican}^2} O_{13} + O'_{13} = S(Y_3) + S(Z+Y_3)

\def\pelican{\textrm{pelican}^2} Y_3 = A+2B+3C+D+K_{9,1}

Only some values of $\def\pelican{\textrm{pelican}^2} Z$ can satisfy simultaneously these equations and, for each candidate value, there is a corresponding set of $\def\pelican{\textrm{pelican}^2} Y_0, Y_1, Y_2, Y_3$ . As we have also the following relations:

\def\pelican{\textrm{pelican}^2} O_0 = S(Y_0)+K_{10,0}

\def\pelican{\textrm{pelican}^2} O_7 = S(Y_1)+K_{10,7}

\def\pelican{\textrm{pelican}^2} O_{10} = S(Y_2)+K_{10,10}

\def\pelican{\textrm{pelican}^2} O_{13} = S(Y_3)+K_{10,13}

we get some possible candidates for $\def\pelican{\textrm{pelican}^2} K_{10,0}, K_{10,7}, K_{10,10}, K_{10,13}$ .

In general, with another fault at the same location and its corresponding faulty output, $\def\pelican{\textrm{pelican}^2} K_{10,0}, K_{10,7}, K_{10,10}, K_{10,13}$ are fully determined. Faulting bytes in the other columns allows to recover the 12 other round key bytes using the same process, which means eight faults (2 per 4 bytes columns) in total are required to break the last round key. The last round key is enough to recover the original AES-128 key because the AES key scheduling is fully invertible without difficulties. In the case of AES-192 and AES-256, breaking the round key of the round before is also required as we will see later.

DFA on White-boxed AES-128

How to Inject the Faults?

It could be done dynamically with an instrumentation framework, a debugger or an emulator as seen in [2] but in simple cases, injecting the fault statically is good enough. In the event of some basic integrity checks, it is often still easier to patch the integrity routine and to apply the fault statically. One big advantage of static faults is that the execution is much faster than when the fault has to be injected dynamically. So let us save dynamic instrumentation for the most difficult cases.

How to inject a fault statically? Simply take a copy the original implementation (or its tables if they are held in a separate file) and change a byte. Because you will do it many times and you do not want to kill your drive, it is usually better to run the attack from a tmpfs volume.

Where to Inject the Faults?

We want to avoid having to find the right locations as this would imply reversing the white-box, which is painful and against our fully automated world domination project. Single-byte faults will therefore be injected at every possible location in the tables. When the tables are not separate files or nicely stored in the .rodata or .data section of the binary but instead heavily merged in the code, we have to inject faults directly in the .text section. This means we have a large chance of modifying the program code and thus breaking the program. One trick in this case is to inject NOP instructions instead of random faults. This limits the number of crashes and results in faster attacks.

Once the fault is injected and the white-box executed, the differences between the faulted output and a reference output help distinguish between several cases:

If the program crashes or takes longer than usual, or the output format is unexpected (empty, garbage...):

We affected something that was not related to the lookup tables but was vital to the program.
If the output is not affected:

The fault was injected in some unused area. Those areas can be pretty big as a white-box implementation uses only a fraction of its table for one input.
If all output bytes are affected:

The fault was injected too early (before the last two MixColumns) or out of the tables bounds (e.g. the loop index). Nevertheless, we know we can simply discard the results.
If one single output byte is affected:

The fault was injected too late (after the last MixColumns). Again we can discard such results.
If exactly four bytes are affected:

We can probably exploit the results.

When four bytes are affected, we can use their pattern to determine in which column the injection occurred. E.g. if output bytes 0, 7, 10 and 13 are affected, we have seen that it can be due to a fault in the first column of the intermediate state (we only developed for a fault in the first byte, $\def\pelican{\textrm{pelican}^2} A$ , but, as the developed equations show, a fault in $\def\pelican{\textrm{pelican}^2} B$ , $\def\pelican{\textrm{pelican}^2} C$ or $\def\pelican{\textrm{pelican}^2} D$ would have affected the same output bytes). Thus, when applying the equations seen before to guess the round key bytes, we have to try these four hypotheses about which byte of the column was actually affected.

One advantage of the white-box setup is that once we have found a nice spot to inject a fault, we can easily inject other faults at the exact same place. In the hardware world this would have required a tricky setup with a trigger to get the timing perfectly right.

Optimization

Still, white-box implementations are large (typically 1 to 4 Mb) and brute-forcing each single byte would take a while. We know that for a given input, only a small portion of the white-box tables is actually used. A better strategy is to start by faulting large areas at once (i.e. faulting all consecutive bytes of a given area) and refine the attack only on the interesting areas. It is a classical divide-and-conquer methodology.

Conclusions on the observed results have to be revised accordingly:

If the program crashes or takes longer than usual or the output format is unexpected:

Divide the area and try again on each half.
If the output is not affected:

The complete area can be ignored.
If all output bytes are affected:

Divide the area and try again on each half.
If one single output byte is affected:

The complete area can be ignored.
If exactly four bytes are affected:

For large areas, there is still quite a risk that more than a single byte got affected in the same column. Therefore, it is better to divide till we identify small areas. Usually we do not even need to go to the byte level to get a successful attack.

The fastest and easiest attacks are against implementations where the tables are "raw", without any meta-data because large faults do not affect usability. When the tables are strongly structured (e.g. Boost serialized tables), faults have a large chance to break the structure and the attack must go on up to the byte level to be able to inject faults that do not affect the meta-data.

Deadpool and JeanGrey

Jointly with our DCA paper [1], we have published on GitHub a few white-box challenges collected here and there, together with scripts to demonstrate the side-channel attacks, under a project called Deadpool.

Since then, we have extended the scripts to demonstrate as well the fault injection attacks. The scripts follow the strategy explained in the previous section and make use of a tmpfs volume. The collected faulty outputs are processed by a new tool called JeanGrey which tries to break the last round key. The final step, going from the last round key back to the AES-128 key, can be achieved with the aes_keyschedule tool located in the Stark project.

The DFA framework is flexible enough to be tuned to each case as we will see through a few examples and it is documented here. All examples are available in the Deadpool project.

NSC2013 Variant

NSC2013 was a white-box challenge with unknown external encodings, but the generator was published afterwards so we could make a variant with clear outputs. Let us remind that this NSC2013 variant was not vulnerable to the DCA attack due to its structure with 8-bit internal encodings.

The tables are "raw" in a separate file so this implementation can be directly broken very fast without any tuning: it takes 5.3s on a laptop and about 420 traces to get the reference output and the 8 usable faulty outputs.

As we have the sources of the generated white-box implementation, the repository contains also a version of the DFA directly applied at source level. But this is an ideal case that could under normal circumstances only be done after a full reversing of the implementation.

Karroumi

The Karroumi white-box is an implementation by Dušan Klinec of a white-box conceived by Mohamed Karroumi. It is written in C++ and makes use of Boost serialization.

As explained earlier, structured data are harder to fault blindly. Therefore we have to tune a parameter of the attack to fault smaller data, up to a single byte. Without any restriction on the address range to fault, the attack takes 162s and about 5800 traces. When restricting the address range to 0x57000 - 0x5A000 the attack takes 7s and about 200 traces.

CHES2016

CHES2016 is a challenge written in C with its tables embedded in the binary.

Using the framework parameters with their default values fails: some traces with the right pattern are found but solving the equations do not yield any valid key candidate. It is difficult to tell why without reversing the entire white-box, but one explanation could be that the injected fault affects more than one byte of the same column of the AES state.

From here, two strategies are possible:

Acquire more traces with a good fault pattern.
Skip the areas where the false positives were found.

Acquiring more traces is easy, just bump up the value of minfaultspercol. With minfaultspercol=200, the key is found in 100s with 20000 traces, out of which 530 present a good fault pattern.

There is no need to fault the entire binary. Looking at the binary structure, we see that the tables are located at file offset 0x21aa0 and are 0x7f020 large:

objdump -h wb_challenge
Sections:
[...]
Idx Name          Size      VMA               LMA               File off  Algn
 24 .data         0007f020  0000000000621aa0  0000000000621aa0  00021aa0  2**5

If we plot the locations where good fault patterns appear, we get:

When restricting the address range to the last blob, in the address range 0x3bab0 - 0x3d300, the attack takes 1.5s and about 70-90 traces to find the right key. Actually restricting the range to addresses above 0x34000 is enough as any of the last three blobs can reveal the key.

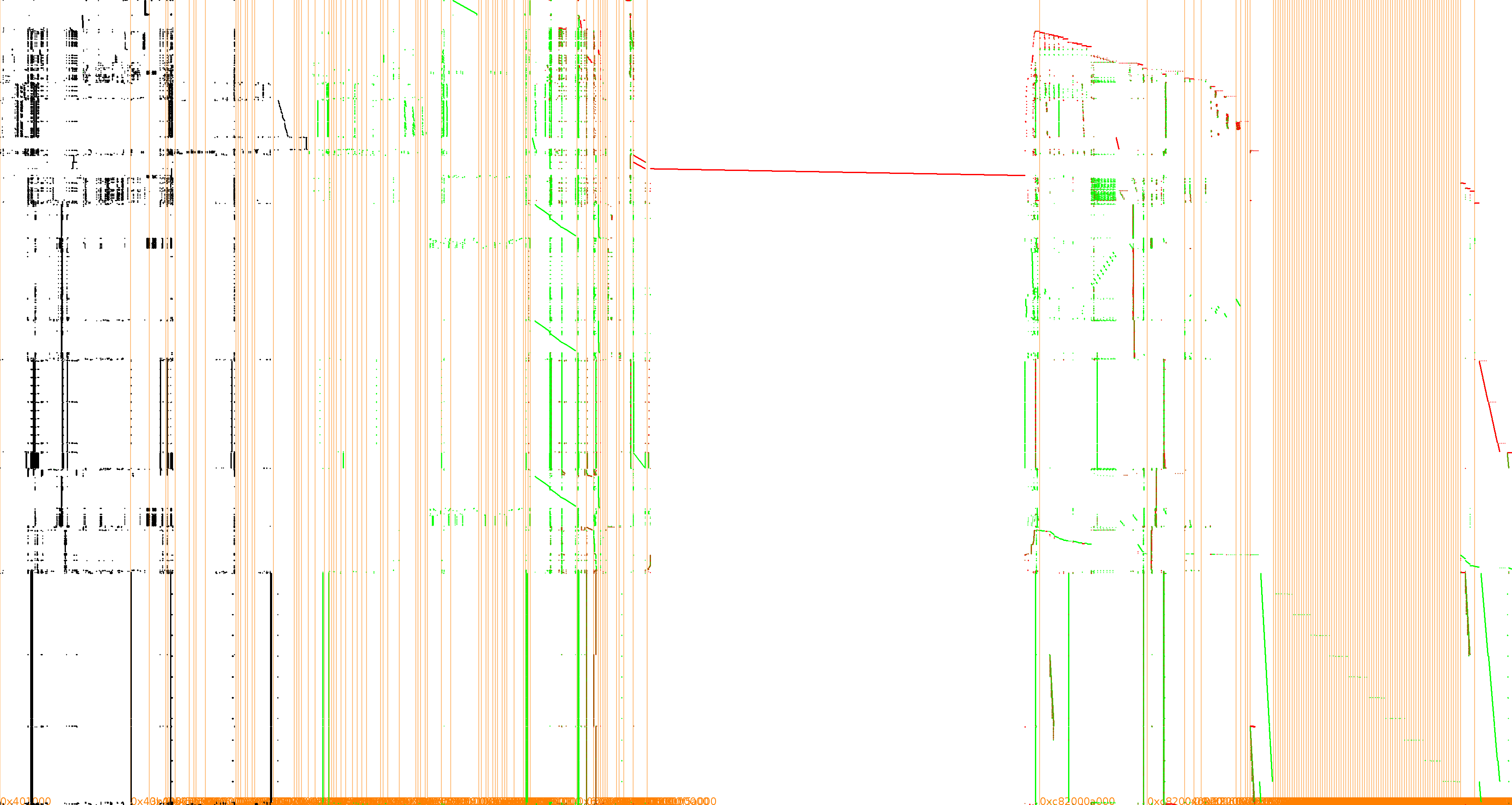
One may find strange that the good spots are pretty early in the tables (roughly between 0x34000 and 0x3e000, while the table ends at 0xa0ac0). Having a look at a visual trace reveals that the tables are actually read backwards, from the highest addresses for the earliest rounds to the lowest addresses for the last rounds. If you have never seen our trace visualizations before (e.g. in DCA context), here is how to read it: Y-axis is time going from the top to the bottom, X-axis is the (virtual) memory layout, instructions are in black, data reads in green and data writes in red.

Visualization of one CHES2016 execution trace

Of course this kind of visualization can also be used to get an idea at what address range to shoot if you have difficulties in getting a successful DFA attack. It was obtained with TraceGraph, which is part of the Tracer project.

With this challenge the source code is made available but it is completely unrolled and very slow to compile, so faulting at source level with some trials and errors is not that easy to automate.

OpenWhiteBox Chow

OpenWhiteBox is an initiative with some similarities with our Deadpool project: it aims at providing white-box implementations and their cryptanalyses. However, as opposed to us, they write their own open source implementations (while we collect existing challenges, sometimes without sources) and they focus on algebraic analyses. In short, it is a nice project complementary to ours! One of their implementation is a Chow construction written in Go.

Unfortunately for us, if Go is neat as source code, it is not the same story when it comes to the underlying execution. To understand what we mean, have a look at the execution trace:

Visualization of one OpenWhiteBox Chow execution trace

Again, as for CHES2016, using the framework parameters with their default values fail because of false positives: traces with a good pattern but that cannot be broken.

We indicate now to the DFA framework that we want to go as deep as single byte faults and we bump up the value of minfaultspercol to 150. The key is finally found in 300s with 34500 traces, out of which 384 present a good fault pattern.

A quick inspection of the logs shows that the faults with a good pattern occur in four distinct regions. If we restrict the injection range to one of those four regions, we see that some are responsible for the false positives while other allow to significantly speed up the attack:

0x3f200 - 0x43a00:

No key found.
0x5b000 - 0x5df00:

No key found.
0x7a100 - 0x7d000:

Key found in 3.2 s.
0x97000 - 0x9a000:

Key found in 2.3 s.

The OpenWhiteBox project features also another implementation based on Xiao and Lai design. So far, it could not be broken with our DFA attack but we still do not know if it is because of the mess caused by Go at runtime (and maybe tuning a DFA properly could succeed in breaking it) or if Xiao-Lai is intrinsically safe against this type of DFA. Here is its execution trace:

Visualization of one OpenWhiteBox Xiao and Lai execution trace

DFA on AES-128 Decryption

Dusart et al. do not mention DFA against decryption in their paper [3] and we were even told once that DFA was only possible on encryption. Let us have a look.

The steps of the last two rounds of an AES-128 decryption are:

InvMixColumns
InvShiftRows
InvSubBytes
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{1}$
InvMixColumns
InvShiftRows
InvSubBytes
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$

The pattern is indeed quite different from the encryption case.

As we did before, let us assume one byte is faulted somewhere between the last two InvMixColumns. The same reasoning used in the encryption case regarding the value and position of the fault can be made, and we can thus work with one byte corrupted just before the last InvMixColumns:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} A & E & I & M \\ B & F & J & N \\ C & G & K & O \\ D & H & L & P \end{pmatrix} \text{and} \begin{pmatrix} X & E & I & M \\ B & F & J & N \\ C & G & K & O \\ D & H & L & P \end{pmatrix}

Which give successively, after InvMixColumns:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} 14A+11B+13C+9D & \cdots & \cdots & \cdots \\ 9A+14B+11C+13D & \cdots & \cdots & \cdots \\ 13A+9B+14C+11D & \cdots & \cdots & \cdots \\ 11A+13B+9C+14D & \cdots & \cdots & \cdots \end{pmatrix} \text{and} \begin{pmatrix} 14X+11B+13C+9D & \cdots & \cdots & \cdots \\ 9X+14B+11C+13D & \cdots & \cdots & \cdots \\ 13X+9B+14C+11D & \cdots & \cdots & \cdots \\ 11X+13B+9C+14D & \cdots & \cdots & \cdots \end{pmatrix}

After InvShiftRows:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} 14A+11B+13C+9D \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad 9A+14B+11C+13D \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad 13A+9B+14C+11D \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad 11A+13B+9C+14D \end{pmatrix} \text{and} \begin{pmatrix} 14A+11B+13C+9D \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad 9A+14B+11C+13D \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad 13A+9B+14C+11D \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad 11A+13B+9C+14D \end{pmatrix}

After InvSubBytes:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} S^{-1}(14A+11B+13C+9D) \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad S^{-1}(9A+14B+11C+13D) \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad S^{-1}(13A+9B+14C+11D) \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S^{-1}(11A+13B+9C+14D) \end{pmatrix} \text{and} \begin{pmatrix} S^{-1}(14X+11B+13C+9D) \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad S^{-1}(9X+14B+11C+13D) \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad S^{-1}(13X+9B+14C+11D) \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S^{-1}(11X+13B+9C+14D) \end{pmatrix}

After AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$ :

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} S^{-1}(14A+11B+13C+9D)+K_{0,0} \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad S^{-1}(9A+14B+11C+13D)+K_{0,5} \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad S^{-1}(13A+9B+14C+11D)+K_{0,10} \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S^{-1}(11A+13B+9C+14D)+K_{0,15} \end{pmatrix} \text{and} \begin{pmatrix} S^{-1}(14X+11B+13C+9D)+K_{0,0} \qquad \cdots \qquad \cdots \qquad \cdots \\ \cdots \qquad S^{-1}(9X+14B+11C+13D)+K_{0,5} \qquad \cdots \qquad \cdots \\ \cdots \qquad \cdots \qquad S^{-1}(13X+9B+14C+11D)+K_{0,10} \qquad \cdots \\ \cdots \qquad \cdots \qquad \cdots \qquad S^{-1}(11X+13B+9C+14D)+K_{0,15} \end{pmatrix}

Thus looking at the first byte of the output, we get for the normal and the faulty cases:

\def\pelican{\textrm{pelican}^2} O_0 = S^{-1}(14A+11B+13C+9D)+K_{0,0} O'_0 = S^{-1}(14X+11B+13C+9D)+K_{0,0}

XORing them:

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S^{-1}(14A+11B+13C+9D)+K_{0,0} + S^{-1}(14X+11B+13C+9D)+K_{0,0}

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S^{-1}(14A+11B+13C+9D) + S^{-1}(14X+11B+13C+9D)

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S^{-1}(14A+11B+13C+9D) + S^{-1}(14X+14A+14A+11B+13C+9D)

If we pose:

\def\pelican{\textrm{pelican}^2} Y_0=14A+11B+13C+9D

\def\pelican{\textrm{pelican}^2} Z=A+X

This becomes:

\def\pelican{\textrm{pelican}^2} O_0 + O'_0 = S^{-1}(Y_0) + S^{-1}(14Z+Y_0)

Similar equations can be written for the three other output bytes affected by the fault:

\def\pelican{\textrm{pelican}^2} O_5 + O'_5 = S^{-1}(Y_1) + S^{-1}(9Z+Y_1)

\def\pelican{\textrm{pelican}^2} Y_1=9A+14B+11C+13D

\def\pelican{\textrm{pelican}^2} O_{10} + O'_{10} = S^{-1}(Y_2) + S^{-1}(13Z+Y_2)

\def\pelican{\textrm{pelican}^2} Y_2=13A+9B+14C+11D

\def\pelican{\textrm{pelican}^2} O_{15} + O'_{15} = S^{-1}(Y_3) + S^{-1}(11Z+Y_3)

\def\pelican{\textrm{pelican}^2} Y_3=11A+13B+9C+14D

\def\pelican{\textrm{pelican}^2} O_0 = S^{-1}(Y_0)+K_{0,0}

\def\pelican{\textrm{pelican}^2} O_5 = S^{-1}(Y_1)+K_{0,5}

\def\pelican{\textrm{pelican}^2} O_{10} = S^{-1}(Y_2)+K_{0,10}

\def\pelican{\textrm{pelican}^2} O_{15} = S^{-1}(Y_3)+K_{0,15}

we get some possible candidates for $\def\pelican{\textrm{pelican}^2} K_{0,0}, K_{0,5}, K_{0,10}, K_{0,15}$ .

The rest is entirely similar to the encryption case, meaning that one more faulty output is required to fully determine $\def\pelican{\textrm{pelican}^2} K_{0,0}, K_{0,5}, K_{0,10}, K_{0,15}$ and thus two faults per column are needed to recover the whole round key. For an AES-128 in decryption, the round key used in the last round is the first round key, which is identical to the AES key. Thus, as opposed to the encryption case, there is no need to reverse the key scheduling.

Again, observing the output tells us if the fault occurred likely at the right place. A nice feature is that the good patterns are different from the ones for an encryption so, facing an unknown white-box, we can tell immediately if it is an encryption or a decryption operation before even trying to recover the key.

AES encryption:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \\ \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \star \quad \cdot \quad \cdot \\ \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \\ \cdot \quad \cdot \quad \star \quad \cdot \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \\ \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \cdot \quad \cdot \quad \star \\ \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \\ \star \quad \cdot \quad \cdot \quad \cdot \end{pmatrix}

AES decryption:

\def\pelican{\textrm{pelican}^2} \begin{pmatrix} \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \star \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \\ \star \quad \cdot \quad \cdot \quad \cdot \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \cdot \quad \star \quad \cdot \\ \cdot \quad \cdot \quad \cdot \quad \star \\ \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \end{pmatrix} \qquad \begin{pmatrix} \cdot \quad \cdot \quad \cdot \quad \star \\ \star \quad \cdot \quad \cdot \quad \cdot \\ \cdot \quad \star \quad \cdot \quad \cdot \\ \cdot \quad \cdot \quad \star \quad \cdot \end{pmatrix}

Deadpool and JeanGrey, bis

Support for AES-128 decryption white-boxes has been added to our tools and demonstrated on the following example.

PlaidCTF2013

PlaidCTF2013 drmless is a challenge that adds to the ubiquitous Unix-like pager less some DRM capabilities to decrypt protected text files with a proper 16-byte license file. This challenge can actually be solved without breaking the white-box key, as the license file is simply applied as a XOR key once the text is decrypted, but let us see anyway if we can break that key.

To avoid spilling garbage in people's terminal if they provide the wrong key, drmless checks if the output seems valid before outputting anything. As we need to have access to the output in every cases, we need to first patch the integrity check, which can be done simply by patching one byte. Moreover, to negate the effect of the license key, we simply use a license key full of zeros, as a XOR with 0x00 will not affect the output. Finally, to automatically retrieve the output from less (which is supposed to be used interactively), we use a few standard less options: -f to force execution on binary files and -E to quit immediately at end-of-file.

There is no large data section in the binary and a quick look at the trace visualization shows indeed that there are only instructions and some stack accesses. drmless operates four blocks by four blocks which explains why the same pattern can be seen four times.

Visualization of one PlaidCTF2013 execution trace (4 AES blocks)

Because we have to fault the code itself, rather than injecting random faults we will inject NOP instructions, i.e. 0x90, and reduce slightly the initial size of the faulted area (as faulting a binary by erasing very large instruction blocks has very little chance to work). With those two minor tunings of the DFA attack, the key is recovered in 17s and 1000 traces (actually about 500 traces, the other half of the executions crashed).

DFA on AES-192 and AES-256

The initial DFA attack([3]) mentions very briefly that you can break an AES-256 implementation by recovering the round key preceding the last one, but it does not explain how.

In the decryption case, once the last round key is known, it is straightforward to inverse the last round and obtain the output of the penultimate round from the output of the last round. This allows us to then perform an attack on the penultimate round. The last round we attack initially is:

InvMixColumns
InvShiftRows
InvSubBytes
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$

Once we obtain $\def\pelican{\textrm{pelican}^2} K_{0}$ we can compute the output of the penultimate round $\def\pelican{\textrm{pelican}^2} O^*=MixColumns(ShiftRow(SubBytes(O+K_{0})))$ and apply the same attack:

InvMixColumns
InvShiftRows
InvSubBytes
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{1}$

Allowing us to recover $\def\pelican{\textrm{pelican}^2} K_{1}$ . Once $\def\pelican{\textrm{pelican}^2} K_{0}$ and $\def\pelican{\textrm{pelican}^2} K_{1}$ are known, their concatenation reveals the AES-256 key or, for AES-192, the concatenation of $\def\pelican{\textrm{pelican}^2} K_{0}$ with the first half of $\def\pelican{\textrm{pelican}^2} K_{1}$ .

However the encryption case is a bit more tricky. Remember that an AES-256 encryption ends with:

SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{13}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{14}$

and assume $\def\pelican{\textrm{pelican}^2} K_{14}$ was found. If we reverse the steps up to the next unknown key, we get:

SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{12}$
SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{13}$

which is not at all the same pattern as for the attack of the first round, we have now an extra MixColumns!

The trick is that most of the AES operations (i.e. all but the SubBytes) are linear and can thus be reordered at will. So we can swap the MixColumns with the AddRoundKey operations:

SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{12}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{13}'$
MixColumns

If we now reverse the MixColumns step as well (we compute $\def\pelican{\textrm{pelican}^2} O^*=InvMixColumns(InvSubBytes(InvShiftRows(O+K_{14})))$ as the output of round 13), we can perform the same attack on:

SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{12}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{13}'$

It should be noted that the key obtained, $\def\pelican{\textrm{pelican}^2} K_{13}'$ , is the key applied before the MixColumns as we swapped both operations. To find the real round key, you must compute $\def\pelican{\textrm{pelican}^2} K_{13}=MixColumns(K_{13}')$ .

Once the last two round keys are known, the AES key schedule can be inverted to reconstruct the AES-192 or AES-256 key. In the event where you do not know if it is an AES-192 or an AES-256 and you do not have a clear plaintext to try, you can assume it is an AES-192, provide one and a half round keys, compute the missing half according to the AES-192 key schedule and see if the other half corresponds to what you got. If not, it is probably an AES-256 (or something weird, as we will see next).

Our aes_keyschedule tool (from Stark project) is flexible and can reconstruct a full key scheduling from any 1, 1.5 or 2 round keys to find the AES key of respectively an AES-128, AES-192 or AES-256.

Weird Case Study: Kryptologik

We discovered recently a white-box challenge apparently written by Mehdi Sotoodeh and called kryptologik.

It demonstrates the usage of a white-box to perform some kind of asymmetric cryptography with a symmetric cipher. The client part is an AES encryption written in JavaScript, to be run in the browser, and the server part takes care of the decryption. His solution is supposed to support AES-128, AES-192 and AES-256 but it is not clear which one was implemented in the challenge.

To apply our attack faster, we decided to first rewrite the JavaScript in C and to offload the tables in an external file. This is easy to do because the white-box operations are simple and virtually the same in many languages so only the initial and final I/O parts must be rewritten for each language. Storing the tables in an external file is, as explained previously, slightly more comfortable to deploy the attack. Note that the author proposes his commercial white-box solutions in JavaScript, C, C++, Python and C# but the demo is only available in JavaScript. Once the challenge is rewritten in C, the DFA framework can be applied with the default parameters. The framework confirms it is an AES encryption and the last round key is found in 8.3s and 600 traces. Assuming it is an AES-128, we revert the key scheduling and... the key we find does not work to decrypt the generated ciphertexts.

Ok, maybe this is an AES-192 or AES-256... To check this we need to crack the previous round key... (actually, this challenge was our motivation to implement the support for AES-192 and AES-256 in our tools, as we had only encountered AES-128 so far). The previous key falls as well. Assuming it is AES-192 and reverting the key schedule, we cannot find a match with the round keys we cracked. Thus this must be AES-256. However this fails too.

The only remaining solution is that this AES is not a standard AES implementation. It cannot use external encodings because the DFA attack would not work in this case. Let us have a look at the trace visualization.

Visualization of one Kryptologik execution trace

This is not very informative... Let us zoom on the stack.

Visualization of one Kryptologik execution trace: the stack

It is not that easy to see but there are 7 very similar patterns, the last one a bit shortened. This could be indicative of 14 rounds, so an AES-256.

At this point we decided to extend the tools to crack all the round keys by DFA. The principle is the same used in the AES-192 and AES-256 but applied recursively up to the first two rounds. For the second one, we do not inject faults in the tables anymore but we directly fault the input as all what is left is:

AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$
SubBytes
ShiftRows
MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{1}$

With the swap of AddRoundKey and MixColumns as we did when cracking all previous rounds it becomes:

AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} InvMixColumns(K_{1})$

To simplify the attack and always use the same equations, we add our own MixColumns after faulting one byte of the input. There are probably other ways to do it but using the same equations is much nicer. So now we are attacking:

MixColumns
AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$
SubBytes
ShiftRows
AddRoundKey $\def\pelican{\textrm{pelican}^2} InvMixColumns(K_{1})$

which looks exactly like the last AES rounds so we can apply once more the same DFA attack, with the addition of our own MixColumns. Once the second key is found, well, we end up with:

AddRoundKey $\def\pelican{\textrm{pelican}^2} K_{0}$

In this case providing a null input reveals immediately the first round key.

The complete attack against all the round keys takes 60s and 9200 traces, out of which 224 exhibit a good faults pattern. So here are revealed for the first time and for your delight the 15 round keys of the Kryptologik challenge :)

roundkeys=[
'0D9BE960C438FF85F656BD48B78A0EE2',
'5A769B843C089BB1357FF628AE897D46',
'46359EFF9EFE9E1B41F1AA45CC250A12',
'AFBF8EFAD8F4878B8CF5E498342885FD',
'FF2C650283CF6605B42FB77E624B798D',
'9002F334E6C6288647B873A6145A15C5',
'DB33A8697D32BAA858D9EBB8FD266B3C',
'772DA79020B322D37C9B86DE70F8C3AA',
'600C5335D45052EB3BC418EAD9C611F3',
'3EC60262C17DE8D51F7E92E90715B965',
'4989783DD27A96D30C13C1ED687838F1',
'42ECC85F8C38152BE2D3F70154F12C8F',
'623247F2EA244F65A691A317F74934F2',
'E3A0F7B76729FB15ABE864512923F937',
'4A41F291E18FAEAFEA926076DDD3586B'
]

We could not find any correlation between the round keys so it was apparently a fake AES-256 where all round keys were diversified and not derived from a single key through the AES key schedule (or it is a modified version of the key schedule but even the elementary XOR relationships between 4-byte words cannot be found).

All that matter is, if we bypass the key scheduling and provide directly this AES-256 expanded key to a standard AES implementation, we can reproduce all aspects of the challenge with its client encryption and its server decryption. The full demo is available in the Deadpool project.

We could attack also the challenge by DCA but it is more hazardous. Let us explain: when a key is found by DFA there is no uncertainty, while when a key is found by DCA, it is just the best candidate among other ones and typically the top candidates are tested against a pair of plaintext and ciphertext. But if all round keys are diversified we cannot validate key candidates and we have to choose one to break the next round key. Any error in our choice will propagate quickly and hurt the attacks on the next rounds. Hopefully, from a quick test on the first round of this challenge with DCA, it seems it leaks quite strongly and the first key candidate stands up quite clearly, so it is probably still doable to break all rounds with DCA in this specific case. The DCA attack on the first round is available in the Deadpool project.

More Experiments

With this new experimental addition to our tool, we can also tackle simple output external encodings such as an additional XOR with an unknown key. Recovering the last round key would reveal a wrong round key, combination of the real round key and the extra unknown key. But we can go on deeper and the next round key(s) to be revealed will be correct. So, using the key scheduling from the intermediate round keys will reveal the real AES key as well as the last round key, and thus the extra unknown key applied to the output.

Back to the PlaidCTF challenge, let us pretend we do not know and do not have control on the license key $\def\pelican{\textrm{pelican}^2} K_{Lic}$ which is XORed with the white-box output to get finally the cleartext.

Attacking the last round by DFA reveals $\def\pelican{\textrm{pelican}^2} K_{0}'=K_{0} \oplus K_{Lic}$ and we still do not know the AES key. Nevertheless we can revert that final round of the decryption and attack the previous round key $\def\pelican{\textrm{pelican}^2} K_{1}$ . It reveals the real second round key $\def\pelican{\textrm{pelican}^2} K_{1}$ from which we can derive all round keys, including the first round key $\def\pelican{\textrm{pelican}^2} K_{0}$ . From there, the license key is simply $\def\pelican{\textrm{pelican}^2} K_{Lic}=K_{0}' \oplus K_{0}$ .

This is similar to the trick used to be able to attack the mutual authentication and key agreement protocol of UTMS and LTE by DPA, despite initial and final XORing of the input/output with an operator secret (OPc), cf. [5].

Countermeasures?

It is not difficult to avoid outputting faulty results or to output garbage in case a fault is detected. But it does not come magically, you have to take care explicitly about DFA when you design a white-box. And still, this has to be done in subtle ways to defeat traditional reverse-engineering as well.

Last Words

All your examples are done on public challenges, I am sure commercial white-boxes are much better and not vulnerable against DFA.

No, definitively no. Some vendors have visibly learned the lesson and did their homework [4] (still, it would be nice to have a challenge to evaluate) but we could apply successfully DFA against several commercial white-box implementations (all the ones we tried actually) such as:

Oops sorry, someone is at the door. Weird, looks like it's the police... Let us commit this draft and see what they want...

[1]	(1, 2) Differential Computation Analysis: Hiding Your White-Box Designs is Not Enough. Joppe W. Bos, Charles Hubain, Wil Michiels and Philippe Teuwen, CHES 2016, available in ePrint 2015/753.

[2]	(1, 2) Unboxing the White-Box. Eloi Sanfelix, Cristofaro Mune and Job de Haas, Blackhat Europe 2015, ICMC16, available in BH16 archives (pdf).

[3]	(1, 2, 3, 4) Differential Fault Analysis on A.E.S. Pierre Dusart, Gilles Letourneux and Olivier Vivolo, ACNS 2003, pages 293-306, available in ePrint 2003/010.

[4]	Evolution of WBC: from table-based implementations to recent designs. Michael J. Wiener, WhibOx 2016, available in WhibOx archives (pdf).

[5]	Small Tweaks Do Not Help: Differential Power Analysis of MILENAGE Implementations in 3G/4G USIM Cards. Junrong Liu, Yu Yu, François-Xavier Standaert, Zheng Guo, Dawu Gu, Wei Sun, Yijie Ge, and Xinjun Xie, ESORICS 2015, available in BH15 archives (pdf).

If you would like to learn more about our security audits and explore how we can help you, get in touch with us!